| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 7 Coordinate Geometry
Welcome to this comprehensive resource dedicated to providing detailed answers and thorough explanations for the Class 10 NCERT Exemplar problems focusing on Coordinate Geometry. These Exemplar questions are specifically designed to move beyond routine formula application, challenging students with more intricate scenarios that demand sophisticated use of coordinate geometry tools. The problems often require significant algebraic manipulation, keen geometric interpretation, and the ability to connect different concepts within challenging contexts. Mastering these solutions will substantially enhance your ability to apply coordinate geometry principles effectively to complex problems.
The solutions meticulously cover the fundamental formulas of coordinate geometry, demonstrating their application in advanced settings. Central to this chapter is the Distance Formula, used to calculate the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ as $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$. The Exemplar problems leverage this formula extensively, not just for finding lengths, but more critically for:
- Proving properties of various geometric shapes by comparing side lengths and diagonal lengths. This includes verifying if a triangle is isosceles or equilateral, or if a quadrilateral is a parallelogram, rectangle, square, or rhombus based on coordinate vertices.
- Checking for the collinearity of three or more points (demonstrating that the sum of distances between consecutive points equals the distance between the endpoints).
Another cornerstone is the Section Formula, which determines the coordinates of a point dividing a line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ in a given ratio $m:n$. For internal division, the coordinates are $(\frac{mx_2+nx_1}{m+n}, \frac{my_2+ny_1}{m+n})$. The solutions explore its application in diverse and demanding situations, such as:
- Finding the coordinates of points dividing a segment in a specific ratio, including calculating coordinates for points of trisection (dividing the segment into three equal parts, requiring ratios $1:2$ and $2:1$).
- Determining the ratio in which a given point (or a line, like the x-axis or y-axis) divides a line segment joining two other points.
- Calculating the coordinates of the centroid of a triangle, which is the point of intersection of medians, given the vertices.
The formula for the Area of a Triangle given the coordinates of its vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ as $\frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|$ is also thoroughly covered. Beyond simple area calculations, the Exemplar problems utilize this formula cleverly, particularly for:
- Establishing the collinearity of three points, leveraging the fact that the area of the triangle formed by collinear points must be $0$.
- Finding the area of quadrilaterals by strategically dividing them into two triangles using a diagonal and summing the areas of the constituent triangles.
Exemplar challenges often integrate these formulas. You might encounter problems requiring you to find vertex coordinates based on midpoint information or other geometric conditions, combine distance and section formulas, or even explore the concept of the locus of a point satisfying specific distance relationships (implicitly touching upon ideas related to circles or perpendicular bisectors). The solutions address all question formats (MCQs, Fill-in-the-Blanks, True/False, Short/Long Answer), providing meticulous calculations, clear formula application, step-by-step algebra, and insightful geometric interpretations, often supported by diagrams. This resource is vital for mastering coordinate geometry at an advanced level.
Sample Question 1 to 3 (Before Exercise 7.1)
Choose the correct answer from the given four options:
Sample Question 1: If the distance between the points (2, –2) and (–1, x) is 5, one of the values of x is
(A) –2
(B) 2
(C) –1
(D) 1
Answer:
Given:
Two points: $(2, -2)$ and $(-1, x)$.
The distance between the points is $5$ units.
To Find:
One of the possible values of $x$.
Solution:
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ in a coordinate plane is given by the distance formula:
$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
Here, let $(x_1, y_1) = (2, -2)$ and $(x_2, y_2) = (-1, x)$. The distance $d = 5$.
Substitute the given values into the distance formula:
$5 = \sqrt{(-1 - 2)^2 + (x - (-2))^2}$
$5 = \sqrt{(-3)^2 + (x + 2)^2}$
$5 = \sqrt{9 + (x + 2)^2}$
To eliminate the square root, square both sides of the equation:
$5^2 = 9 + (x + 2)^2$
$25 = 9 + (x + 2)^2$}
Subtract 9 from both sides:
$25 - 9 = (x + 2)^2$
$16 = (x + 2)^2$
Take the square root of both sides:
$\pm \sqrt{16} = x + 2$
$\pm 4 = x + 2$
This gives two possible cases for the value of $x$:
Case 1: $4 = x + 2$
$x = 4 - 2$
$x = 2$
Case 2: $-4 = x + 2$
$x = -4 - 2$
$x = -6$
The possible values for $x$ are $2$ and $-6$. We need to choose one of these values from the given options.
Looking at the options:
(A) –2
(B) 2
(C) –1
(D) 1
The value $2$ is present in option (B).
Answer:
One of the values of $x$ is $2$.
The correct option is (B).
Sample Question 2: The mid-point of the line segment joining the points A (–2, 8) and B (– 6, – 4) is
(A) (– 4, – 6)
(B) (2, 6)
(C) (– 4, 2)
(D) (4, 2)
Answer:
Given:
Point A = $(-2, 8)$.
Point B = $(-6, -4)$.
To Find:
The coordinates of the mid-point of the line segment joining A and B.
Solution:
The coordinates of the mid-point of a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ are given by the mid-point formula:
Mid-point $(x, y) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$
Here, $(x_1, y_1) = (-2, 8)$ and $(x_2, y_2) = (-6, -4)$.
x-coordinate of the mid-point:
$x = \frac{-2 + (-6)}{2} = \frac{-2 - 6}{2} = \frac{-8}{2} = -4$
y-coordinate of the mid-point:
$y = \frac{8 + (-4)}{2} = \frac{8 - 4}{2} = \frac{4}{2} = 2$
So, the coordinates of the mid-point are $(-4, 2)$.
Answer:
The mid-point of the line segment is $(-4, 2)$.
The correct option is (C).
Sample Question 3: The points A (9, 0), B (9, 6), C (–9, 6) and D (–9, 0) are the vertices of a
(A) square
(B) rectangle
(C) rhombus
(D) trapezium
Answer:
Given:
The vertices of a quadrilateral ABCD are A$(9, 0)$, B$(9, 6)$, C$(-9, 6)$, and D$(-9, 0)$.
To Find:
The type of quadrilateral formed by the given vertices.
Solution:
We will find the length of each side and the lengths of the diagonals using the distance formula. The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Length of AB:
AB = $\sqrt{(9-9)^2 + (6-0)^2} = \sqrt{0^2 + 6^2} = \sqrt{0 + 36} = \sqrt{36} = 6$ units.
Length of BC:
BC = $\sqrt{(-9-9)^2 + (6-6)^2} = \sqrt{(-18)^2 + 0^2} = \sqrt{324 + 0} = \sqrt{324} = 18$ units.
Length of CD:
CD = $\sqrt{(-9-(-9))^2 + (0-6)^2} = \sqrt{(-9+9)^2 + (-6)^2} = \sqrt{0^2 + 36} = \sqrt{36} = 6$ units.
Length of DA:
DA = $\sqrt{(9-(-9))^2 + (0-0)^2} = \sqrt{(9+9)^2 + 0^2} = \sqrt{18^2 + 0} = \sqrt{324} = 18$ units.
We observe that AB = CD = 6 and BC = DA = 18. Since opposite sides are equal, the quadrilateral ABCD is a parallelogram.
Now, let's find the lengths of the diagonals.
Length of diagonal AC:
AC = $\sqrt{(-9-9)^2 + (6-0)^2} = \sqrt{(-18)^2 + 6^2} = \sqrt{324 + 36} = \sqrt{360}$ units.
Length of diagonal BD:
BD = $\sqrt{(-9-9)^2 + (0-6)^2} = \sqrt{(-18)^2 + (-6)^2} = \sqrt{324 + 36} = \sqrt{360}$ units.
We observe that AC = BD = $\sqrt{360}$.
Since the opposite sides are equal and the diagonals are equal, the parallelogram ABCD is a rectangle. It is not a square because the adjacent sides (e.g., AB and BC) are not equal in length ($6 \neq 18$). It is not a rhombus because adjacent sides are not equal. It is not just a trapezium as both pairs of opposite sides are parallel (verified by slopes: AB and CD are vertical, BC and DA are horizontal, hence perpendicular sides and 4 right angles).
Answer:
The points A (9, 0), B (9, 6), C (–9, 6) and D (–9, 0) are the vertices of a rectangle.
The correct option is (B).
Exercise 7.1
Choose the correct answer from the given four options:
Question 1. The distance of the point P (2, 3) from the x-axis is
(A) 2
(B) 3
(C) 1
(D) 5
Answer:
Given:
The point P with coordinates $(2, 3)$.
To Find:
The distance of the point P from the x-axis.
Solution:
The distance of any point $(x, y)$ from the x-axis is given by the absolute value of its y-coordinate, which is $|y|$.
In this case, the point is P $(2, 3)$.
The x-coordinate is $x = 2$ and the y-coordinate is $y = 3$.
The distance of the point P from the x-axis is $|y| = |3| = 3$ units.
Answer:
The distance of the point P (2, 3) from the x-axis is $3$.
The correct option is (B).
Question 2. The distance between the points A (0, 6) and B (0, –2) is
(A) 6
(B) 8
(C) 4
(D) 2
Answer:
Given:
Point A = $(0, 6)$.
Point B = $(0, -2)$.
To Find:
The distance between points A and B.
Solution:
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ in a coordinate plane is given by the distance formula:
$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
Here, let $(x_1, y_1) = (0, 6)$ and $(x_2, y_2) = (0, -2)$.
Substitute the given values into the distance formula:
$d = \sqrt{(0 - 0)^2 + (-2 - 6)^2}$
$d = \sqrt{(0)^2 + (-8)^2}$
$d = \sqrt{0 + 64}$
$d = \sqrt{64}$
$d = 8$ units.
Alternatively, since both points have the same x-coordinate (0), they lie on the y-axis. The distance between them is the absolute difference of their y-coordinates:
$d = |y_2 - y_1| = |-2 - 6| = |-8| = 8$ units.
Or, $d = |y_1 - y_2| = |6 - (-2)| = |6 + 2| = |8| = 8$ units.
Answer:
The distance between the points A (0, 6) and B (0, –2) is $8$.
The correct option is (B).
Question 3. The distance of the point P (–6, 8) from the origin is
(A) 8
(B) 2$\sqrt{7}$
(C) 10
(D) 6
Answer:
Given:
The point P with coordinates $(-6, 8)$.
The origin O with coordinates $(0, 0)$.
To Find:
The distance of the point P from the origin.
Solution:
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ in a coordinate plane is given by the distance formula:
$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
To find the distance of a point P$(x, y)$ from the origin O$(0, 0)$, we can use the simplified formula:
$d = \sqrt{x^2 + y^2}$
Here, the point is P $(-6, 8)$. So, $x = -6$ and $y = 8$.
Substitute these values into the formula:
$d = \sqrt{(-6)^2 + (8)^2}$
$d = \sqrt{36 + 64}$
$d = \sqrt{100}$
$d = 10$ units.
Answer:
The distance of the point P (–6, 8) from the origin is $10$.
The correct option is (C).
Question 4. The distance between the points (0, 5) and (–5, 0) is
(A) 5
(B) 5$\sqrt{2}$
(C) 2$\sqrt{5}$
(D) 10
Answer:
Given:
Point A = $(0, 5)$.
Point B = $(-5, 0)$.
To Find:
The distance between points A and B.
Solution:
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ in a coordinate plane is given by the distance formula:
$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
Here, let $(x_1, y_1) = (0, 5)$ and $(x_2, y_2) = (-5, 0)$.
Substitute the given values into the distance formula:
$d = \sqrt{(-5 - 0)^2 + (0 - 5)^2}$
$d = \sqrt{(-5)^2 + (-5)^2}$
$d = \sqrt{25 + 25}$
$d = \sqrt{50}$
To simplify $\sqrt{50}$, find the prime factorization of 50:
$50 = 2 \times 25 = 2 \times 5^2$
So, $\sqrt{50} = \sqrt{5^2 \times 2} = \sqrt{5^2} \times \sqrt{2} = 5\sqrt{2}$ units.
Answer:
The distance between the points (0, 5) and (–5, 0) is $5\sqrt{2}$.
The correct option is (B).
Question 5. AOBC is a rectangle whose three vertices are vertices A (0, 3), O (0, 0) and B (5, 0). The length of its diagonal is
(A) 5
(B) 3
(C) $\sqrt{34}$
(D) 4
Answer:
Given:
Three vertices of a rectangle AOBC are A$(0, 3)$, O$(0, 0)$, and B$(5, 0)$.
To Find:
The length of the diagonal of the rectangle.
Solution:
Let the vertices of the rectangle be A$(0, 3)$, O$(0, 0)$, and B$(5, 0)$. Since O is the origin and the coordinates of A and B are $(0, 3)$ and $(5, 0)$, the segment OA lies along the y-axis and the segment OB lies along the x-axis.
The length of OA = $\sqrt{(0-0)^2 + (3-0)^2} = \sqrt{0^2 + 3^2} = \sqrt{9} = 3$ units.
The length of OB = $\sqrt{(5-0)^2 + (0-0)^2} = \sqrt{5^2 + 0^2} = \sqrt{25} = 5$ units.
Since OA is along the y-axis and OB is along the x-axis, $\angle{\text{AOB}} = 90^\circ$. This means OA and OB are adjacent sides of the rectangle meeting at the vertex O.
Let the fourth vertex be C$(x, y)$. In a rectangle, the opposite sides are equal and parallel. Since OA and OB are adjacent sides at O, the vertices are likely in the order O, A, C, B (or O, B, C, A).
Assuming the vertices are in the order O(0,0), A(0,3), C(x,y), B(5,0) or O(0,0), B(5,0), C(x,y), A(0,3), given the question names the rectangle AOBC, it suggests the vertices in order are A, O, B, C. However, with A(0,3), O(0,0), B(5,0), the segment AB is a diagonal (length $\sqrt{34}$). If AO and OB were sides, the fourth vertex C would be at (5,3). Let's check the diagonal lengths for the rectangle formed by O(0,0), A(0,3), B(5,0) and C(5,3).
The vertices are O$(0,0)$, A$(0,3)$, B$(5,0)$ and C$(5,3)$.
The diagonals of this rectangle are AB and OC.
Length of diagonal AB = $\sqrt{(5-0)^2 + (0-3)^2} = \sqrt{5^2 + (-3)^2} = \sqrt{25 + 9} = \sqrt{34}$ units.
Length of diagonal OC = $\sqrt{(5-0)^2 + (3-0)^2} = \sqrt{5^2 + 3^2} = \sqrt{25 + 9} = \sqrt{34}$ units.
Both diagonals have the same length, which is expected for a rectangle. The length of the diagonal is $\sqrt{34}$.
Answer:
The length of its diagonal is $\sqrt{34}$.
The correct option is (C).
Question 6. The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
(A) 5
(B) 12
(C) 11
(D) 7 + $\sqrt{5}$
Answer:
Given:
The vertices of the triangle are A$(0, 4)$, O$(0, 0)$, and B$(3, 0)$.
To Find:
The perimeter of the triangle with the given vertices.
Solution:
To find the perimeter of the triangle, we need to find the length of each of its sides. We will use the distance formula to calculate the length between each pair of vertices. The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the formula:
$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
Calculate the length of side AO:
Using points A$(0, 4)$ and O$(0, 0)$:
$AO = \sqrt{(0-0)^2 + (0-4)^2} = \sqrt{0^2 + (-4)^2} = \sqrt{0 + 16} = \sqrt{16} = 4$ units.
Calculate the length of side OB:
Using points O$(0, 0)$ and B$(3, 0)$:
$OB = \sqrt{(3-0)^2 + (0-0)^2} = \sqrt{3^2 + 0^2} = \sqrt{9 + 0} = \sqrt{9} = 3$ units.
Calculate the length of side AB:
Using points A$(0, 4)$ and B$(3, 0)$:
$AB = \sqrt{(3-0)^2 + (0-4)^2} = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5$ units.
The perimeter of the triangle is the sum of the lengths of its three sides (AO + OB + AB).
Perimeter = $4 + 3 + 5 = 12$ units.
Answer:
The perimeter of the triangle with vertices (0, 4), (0, 0) and (3, 0) is $12$.
The correct option is (B).
Question 7. The area of a triangle with vertices A (3, 0), B (7, 0) and C (8, 4) is
(A) 14
(B) 28
(C) 8
(D) 6
Answer:
Given:
The vertices of the triangle are A$(3, 0)$, B$(7, 0)$, and C$(8, 4)$.
To Find:
The area of the triangle with the given vertices.
Solution:
We can calculate the area of a triangle using the coordinates of its vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ using the formula:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Let A$(3, 0) = (x_1, y_1)$, B$(7, 0) = (x_2, y_2)$, and C$(8, 4) = (x_3, y_3)$.
Substitute the coordinates into the formula:
Area $= \frac{1}{2} |3(0 - 4) + 7(4 - 0) + 8(0 - 0)|$
Area $= \frac{1}{2} |3(-4) + 7(4) + 8(0)|$
Area $= \frac{1}{2} |-12 + 28 + 0|$
Area $= \frac{1}{2} |16|$
Area $= \frac{1}{2} \times 16$
Area $= 8$ square units.
Alternate Solution:
Observe that points A $(3, 0)$ and B $(7, 0)$ lie on the x-axis since their y-coordinates are 0. The side AB is a horizontal line segment on the x-axis.
The length of the base AB can be calculated as the distance between A and B:
Base AB = $|7 - 3| = |4| = 4$ units.
The height of the triangle with respect to the base AB is the perpendicular distance from the vertex C $(8, 4)$ to the line containing AB (which is the x-axis, $y=0$).
The distance of a point $(x, y)$ from the x-axis is $|y|$.
Height = Distance of C$(8, 4)$ from x-axis = $|4| = 4$ units.
The area of a triangle can also be calculated using the formula:
Area $= \frac{1}{2} \times \text{base} \times \text{height}$
Area $= \frac{1}{2} \times 4 \times 4$
Area $= \frac{1}{2} \times 16$
Area $= 8$ square units.
Both methods yield the same result.
Answer:
The area of a triangle with vertices A (3, 0), B (7, 0) and C (8, 4) is $8$.
The correct option is (C).
Question 8. The points (–4, 0), (4, 0), (0, 3) are the vertices of a
(A) right triangle
(B) isosceles triangle
(C) equilateral triangle
(D) scalene triangle
Answer:
Given:
The vertices of the triangle are A$(-4, 0)$, B$(4, 0)$, and C$(0, 3)$.
To Find:
The type of triangle formed by the given vertices.
Solution:
To determine the type of triangle, we need to calculate the lengths of its sides. We will use the distance formula. The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Calculate the length of side AB:
Using points A$(-4, 0)$ and B$(4, 0)$:
$AB = \sqrt{(4 - (-4))^2 + (0 - 0)^2} = \sqrt{(4+4)^2 + 0^2} = \sqrt{8^2 + 0} = \sqrt{64} = 8$ units.
Calculate the length of side BC:
Using points B$(4, 0)$ and C$(0, 3)$:
$BC = \sqrt{(0 - 4)^2 + (3 - 0)^2} = \sqrt{(-4)^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5$ units.
Calculate the length of side AC:
Using points A$(-4, 0)$ and C$(0, 3)$:
$AC = \sqrt{(0 - (-4))^2 + (3 - 0)^2} = \sqrt{(0+4)^2 + 3^2} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5$ units.
We have the side lengths: AB = 8, BC = 5, and AC = 5.
Comparing the side lengths:
AB = 8
BC = 5
AC = 5
Since two sides (BC and AC) have equal lengths, the triangle is an isosceles triangle.
Let's also check if it is a right triangle using the Pythagorean theorem. We check if the square of the longest side is equal to the sum of the squares of the other two sides.
$AB^2 = 8^2 = 64$
$BC^2 = 5^2 = 25$
$AC^2 = 5^2 = 25$
Check if $AB^2 = BC^2 + AC^2$: $64 = 25 + 25 = 50$. Since $64 \neq 50$, it is not a right triangle with the right angle at C.
Check other combinations: $BC^2 + AB^2 = 25 + 64 = 89 \neq AC^2$. $AC^2 + AB^2 = 25 + 64 = 89 \neq BC^2$.
So, the triangle is not a right triangle.
Since not all sides are equal, it is not an equilateral triangle.
Since two sides are equal, it is not a scalene triangle (where all sides are different).
Therefore, the triangle is an isosceles triangle.
Answer:
The points (–4, 0), (4, 0), (0, 3) are the vertices of an isosceles triangle.
The correct option is (B).
Question 9. The point which divides the line segment joining the points (7, –6) and (3, 4) in ratio 1 : 2 internally lies in the
(A) I quadrant
(B) II quadrant
(C) III quadrant
(D) IV quadrant
Answer:
Given:
Point A = $(7, -6)$.
Point B = $(3, 4)$.
The line segment AB is divided internally in the ratio $1 : 2$. Let the ratio be $m : n = 1 : 2$.
To Find:
The quadrant in which the point dividing the line segment internally lies.
Solution:
Let the point that divides the line segment joining A$(x_1, y_1)$ and B$(x_2, y_2)$ internally in the ratio $m : n$ be P$(x, y)$. The coordinates of P are given by the section formula for internal division:
$x = \frac{m x_2 + n x_1}{m+n}$
$y = \frac{m y_2 + n y_1}{m+n}$
Here, $(x_1, y_1) = (7, -6)$, $(x_2, y_2) = (3, 4)$, $m = 1$, and $n = 2$.
Calculate the x-coordinate of the point P:
$x = \frac{(1 \times 3) + (2 \times 7)}{1 + 2}$
$x = \frac{3 + 14}{3}$
$x = \frac{17}{3}$
Calculate the y-coordinate of the point P:
$y = \frac{(1 \times 4) + (2 \times (-6))}{1 + 2}$
$y = \frac{4 - 12}{3}$
$y = \frac{-8}{3}$
The coordinates of the point P are $\left(\frac{17}{3}, -\frac{8}{3}\right)$.
Now, we determine the quadrant based on the signs of the coordinates:
The x-coordinate is $\frac{17}{3}$. Since $17$ and $3$ are both positive, $\frac{17}{3} > 0$.
The y-coordinate is $-\frac{8}{3}$. Since $8$ and $3$ are both positive, $\frac{8}{3} > 0$, but the negative sign makes $-\frac{8}{3} < 0$.
A point with a positive x-coordinate $(x > 0)$ and a negative y-coordinate $(y < 0)$ lies in the IV quadrant.
Answer:
The point which divides the line segment joining the points (7, –6) and (3, 4) in ratio 1 : 2 internally lies in the IV quadrant.
The correct option is (D).
Question 10. The point which lies on the perpendicular bisector of the line segment joining the points A (–2, –5) and B (2, 5) is
(A) (0, 0)
(B) (0, 2)
(C) (2, 0)
(D) (–2, 0)
Answer:
Given:
Point A = $(-2, -5)$.
Point B = $(2, 5)$.
To Find:
The point which lies on the perpendicular bisector of the line segment AB.
Solution:
The perpendicular bisector of a line segment is the line that passes through the midpoint of the segment and is perpendicular to it.
Any point on the perpendicular bisector is equidistant from the two endpoints of the line segment. So, if a point P$(x, y)$ lies on the perpendicular bisector of AB, then the distance PA must be equal to the distance PB.
Let's check the distance from each given option to points A and B.
Distance formula: $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
Point A = $(-2, -5)$, Point B = $(2, 5)$.
Check option (A): Point P$(0, 0)$.
Distance PA = $\sqrt{(0 - (-2))^2 + (0 - (-5))^2} = \sqrt{(0+2)^2 + (0+5)^2} = \sqrt{2^2 + 5^2} = \sqrt{4 + 25} = \sqrt{29}$
Distance PB = $\sqrt{(0 - 2)^2 + (0 - 5)^2} = \sqrt{(-2)^2 + (-5)^2} = \sqrt{4 + 25} = \sqrt{29}$
Since PA = PB = $\sqrt{29}$, the point (0, 0) is equidistant from A and B. Therefore, the point (0, 0) lies on the perpendicular bisector of AB.
We can also verify this by finding the equation of the perpendicular bisector.
Midpoint of AB: M $\left(\frac{-2+2}{2}, \frac{-5+5}{2}\right) = \left(\frac{0}{2}, \frac{0}{2}\right) = (0, 0)$.
The slope of the line segment AB:
$m_{\text{AB}} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{5 - (-5)}{2 - (-2)} = \frac{5+5}{2+2} = \frac{10}{4} = \frac{5}{2}$
The slope of the perpendicular bisector is the negative reciprocal of the slope of AB.
$m_{\perp} = -\frac{1}{m_{\text{AB}}} = -\frac{1}{5/2} = -\frac{2}{5}$
The perpendicular bisector passes through the midpoint (0, 0). Using the point-slope form $y - y_1 = m(x - x_1)$, with $(x_1, y_1) = (0, 0)$ and $m = -\frac{2}{5}$:
$y - 0 = -\frac{2}{5}(x - 0)$
$y = -\frac{2}{5}x$
The equation of the perpendicular bisector is $y = -\frac{2}{5}x$ or $2x + 5y = 0$.
Now, check which option satisfies this equation.
(A) (0, 0): $2(0) + 5(0) = 0 + 0 = 0$. Satisfies the equation.
(B) (0, 2): $2(0) + 5(2) = 0 + 10 = 10 \neq 0$. Does not satisfy.
(C) (2, 0): $2(2) + 5(0) = 4 + 0 = 4 \neq 0$. Does not satisfy.
(D) (–2, 0): $2(-2) + 5(0) = -4 + 0 = -4 \neq 0$. Does not satisfy.
Both methods confirm that the point (0, 0) lies on the perpendicular bisector.
Answer:
The point which lies on the perpendicular bisector of the line segment joining the points A (–2, –5) and B (2, 5) is (0, 0).
The correct option is (A).
Question 11. The fourth vertex D of a parallelogram ABCD whose three vertices are A (–2, 3), B (6, 7) and C (8, 3) is
(A) (0, 1)
(B) (0, –1)
(C) (–1, 0)
(D) (1, 0)
Answer:
Given:
Three vertices of a parallelogram ABCD are A$(-2, 3)$, B$(6, 7)$, and C$(8, 3)$.
To Find:
The coordinates of the fourth vertex D.
Solution:
In a parallelogram, the diagonals bisect each other. This means the midpoint of the diagonal AC is the same as the midpoint of the diagonal BD.
Let the coordinates of the fourth vertex D be $(x, y)$.
The midpoint of a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Midpoint of diagonal AC (joining A$(-2, 3)$ and C$(8, 3)$):
Midpoint of AC = $\left(\frac{-2 + 8}{2}, \frac{3 + 3}{2}\right) = \left(\frac{6}{2}, \frac{6}{2}\right) = (3, 3)$
Midpoint of diagonal BD (joining B$(6, 7)$ and D$(x, y)$):
Midpoint of BD = $\left(\frac{6 + x}{2}, \frac{7 + y}{2}\right)$
Since the midpoints of AC and BD are the same:
$\left(\frac{6 + x}{2}, \frac{7 + y}{2}\right) = (3, 3)$
Equating the x-coordinates:
$\frac{6 + x}{2} = 3$
$6 + x = 3 \times 2$
$6 + x = 6$
$x = 6 - 6$
$x = 0$
Equating the y-coordinates:
$\frac{7 + y}{2} = 3$
$7 + y = 3 \times 2$
$7 + y = 6$
$y = 6 - 7$
$y = -1$
So, the coordinates of the fourth vertex D are $(0, -1)$.
Answer:
The fourth vertex D of the parallelogram is $(0, -1)$.
The correct option is (B).
Question 12. If the point P (2, 1) lies on the line segment joining points A (4, 2) and B (8, 4), then
(A) AP = $\frac{1}{3}$ AB
(B) AP = PB
(C) PB = $\frac{1}{3}$ AB
(D) AP = $\frac{1}{2}$ AB
Answer:
Given:
Point A = $(4, 2)$.
Point B = $(8, 4)$.
Point P = $(2, 1)$.
The point P lies on the line segment joining A and B.
To Find:
The relationship between the lengths AP, PB, and AB.
Solution:
We need to calculate the distance between each pair of points using the distance formula:
$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
Calculate the distance AB (length of the segment AB):
Using points A$(4, 2)$ and B$(8, 4)$:
$AB = \sqrt{(8-4)^2 + (4-2)^2} = \sqrt{4^2 + 2^2} = \sqrt{16 + 4} = \sqrt{20}$
$AB = \sqrt{4 \times 5} = 2\sqrt{5}$ units.
Calculate the distance AP (length of the segment AP):
Using points A$(4, 2)$ and P$(2, 1)$:
$AP = \sqrt{(2-4)^2 + (1-2)^2} = \sqrt{(-2)^2 + (-1)^2} = \sqrt{4 + 1} = \sqrt{5}$ units.
Calculate the distance PB (length of the segment PB):
Using points P$(2, 1)$ and B$(8, 4)$:
$PB = \sqrt{(8-2)^2 + (4-1)^2} = \sqrt{6^2 + 3^2} = \sqrt{36 + 9} = \sqrt{45}$
$PB = \sqrt{9 \times 5} = 3\sqrt{5}$ units.
Now, let's compare the calculated distances:
AP = $\sqrt{5}$
AB = $2\sqrt{5}$
PB = $3\sqrt{5}$
We observe that the length AB is twice the length AP:
$AB = 2 \times AP$
$2\sqrt{5} = 2 \times \sqrt{5}$
This implies that $AP = \frac{1}{2} AB$.
Let's also check the relationship between AP, PB, and AB. If P lies on the line segment AB, the distances should satisfy $AP + PB = AB$.
$AP + PB = \sqrt{5} + 3\sqrt{5} = 4\sqrt{5}$.
However, $AB = 2\sqrt{5}$. Since $4\sqrt{5} \neq 2\sqrt{5}$, the point P(2,1) does not lie *between* A(4,2) and B(8,4). It is collinear (as slopes $\frac{1-2}{2-4} = \frac{1}{2}$, $\frac{4-1}{8-2} = \frac{1}{2}$, $\frac{4-2}{8-4} = \frac{1}{2}$ are equal), but the order is P-A-B, not A-P-B.
Despite the phrasing "lies on the line segment joining", the relationship between the lengths derived from the given coordinates is $AP = \frac{1}{2} AB$, which matches option (D).
Answer:
Based on the given coordinates, the relationship between AP and AB is $AP = \frac{1}{2} AB$.
The correct option is (D).
Question 13. If P $\left( \frac{a}{3} , 4 \right)$ is the mid-point of the line segment joining the points Q (– 6, 5) and R (– 2, 3), then the value of a is
(A) – 4
(B) – 12
(C) 12
(D) – 6
Answer:
Given:
Point Q = $(-6, 5)$.
Point R = $(-2, 3)$.
Point P = $\left(\frac{a}{3}, 4\right)$ is the mid-point of the line segment QR.
To Find:
The value of $a$.
Solution:
The coordinates of the mid-point of a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ are given by the mid-point formula:
Mid-point $(x, y) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$
Here, the mid-point is P $\left(\frac{a}{3}, 4\right)$, and the endpoints are Q $(-6, 5)$ and R $(-2, 3)$.
Let $(x_1, y_1) = (-6, 5)$ and $(x_2, y_2) = (-2, 3)$.
The coordinates of the mid-point are:
$x = \frac{-6 + (-2)}{2} = \frac{-6 - 2}{2} = \frac{-8}{2} = -4$
$y = \frac{5 + 3}{2} = \frac{8}{2} = 4$
So, the mid-point of QR is $(-4, 4)$.
We are given that the mid-point P is $\left(\frac{a}{3}, 4\right)$.
By comparing the coordinates of the mid-point P, we have:
The x-coordinate: $\frac{a}{3} = -4$
The y-coordinate: $4 = 4$}
From the equation for the x-coordinate, we can solve for $a$:
$\frac{a}{3} = -4$
Multiply both sides by 3:
$a = -4 \times 3$
$a = -12$
The y-coordinate equation $4 = 4$ is consistent, confirming that the given information is valid.
Answer:
The value of $a$ is $-12$.
The correct option is (B).
Question 14. The perpendicular bisector of the line segment joining the points A (1, 5) and B (4, 6) cuts the y-axis at
(A) (0, 13)
(B) (0, –13)
(C) (0, 12)
(D) (13, 0)
Answer:
Given:
Point A = $(1, 5)$.
Point B = $(4, 6)$.
To Find:
The point where the perpendicular bisector of the line segment joining A and B cuts the y-axis.
Solution:
The perpendicular bisector of a line segment passes through the midpoint of the segment and is perpendicular to it.
First, let's find the coordinates of the midpoint M of the line segment AB. The midpoint formula for points $(x_1, y_1)$ and $(x_2, y_2)$ is $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Midpoint M = $\left(\frac{1 + 4}{2}, \frac{5 + 6}{2}\right) = \left(\frac{5}{2}, \frac{11}{2}\right)$.
Next, let's find the slope of the line segment AB. The slope formula for points $(x_1, y_1)$ and $(x_2, y_2)$ is $m = \frac{y_2 - y_1}{x_2 - x_1}$.
Slope of AB, $m_{\text{AB}} = \frac{6 - 5}{4 - 1} = \frac{1}{3}$.
The perpendicular bisector is perpendicular to AB. The slope of a line perpendicular to another line with slope $m$ is $-\frac{1}{m}$ (if $m \neq 0$).
Slope of the perpendicular bisector, $m_{\perp} = -\frac{1}{m_{\text{AB}}} = -\frac{1}{1/3} = -3$.
Now we have the slope of the perpendicular bisector ($m_{\perp} = -3$) and a point it passes through (the midpoint M $\left(\frac{5}{2}, \frac{11}{2}\right)$). We can find the equation of the perpendicular bisector using the point-slope form of a linear equation: $y - y_1 = m(x - x_1)$.
$y - \frac{11}{2} = -3\left(x - \frac{5}{2}\right)$
$y - \frac{11}{2} = -3x + 3 \times \frac{5}{2}$
$y - \frac{11}{2} = -3x + \frac{15}{2}$
$y = -3x + \frac{15}{2} + \frac{11}{2}$
$y = -3x + \frac{15 + 11}{2}$}
$y = -3x + \frac{26}{2}$}
$y = -3x + 13$
This is the equation of the perpendicular bisector.
To find where this line cuts the y-axis, we set the x-coordinate to $0$ (since any point on the y-axis has an x-coordinate of 0).
Substitute $x = 0$ into the equation:
$y = -3(0) + 13$
$y = 0 + 13$
$y = 13$
So, the perpendicular bisector cuts the y-axis at the point $(0, 13)$.
Answer:
The perpendicular bisector of the line segment joining the points A (1, 5) and B (4, 6) cuts the y-axis at (0, 13).
The correct option is (A).
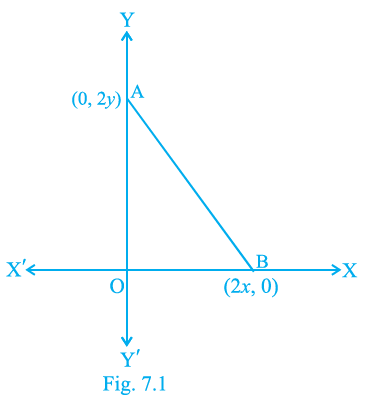
Question 15. The coordinates of the point which is equidistant from the three vertices of the Δ AOB as shown in the Fig. 7.1 is
(A) (x, y)
(B) (y, x)
(C) $\frac{x}{2}$ , $\frac{y}{2}$
(D) $\frac{y}{2}$ , $\frac{x}{2}$
Answer:
Given:
The vertices of $\triangle{\text{AOB}}$ are A, O, and B as shown in Fig. 7.1.
Although the figure is not provided, based on the common representation in such problems and the structure of the options involving $\frac{x}{2}$ and $\frac{y}{2}$, we can infer that O is the origin $(0, 0)$, A is a point on one axis, and B is a point on the other axis, forming a right-angled triangle at the origin.
Let the vertices be O$(0, 0)$, A$(x', 0)$, and B$(0, y')$. Here $x'$ and $y'$ represent the coordinates of A and B along the axes. The options use $x$ and $y$, so it is likely that the coordinates of A are $(x, 0)$ and B are $(0, y)$ in the context of the figure.
Vertices are O$(0, 0)$, A$(x, 0)$, and B$(0, y)$.
This forms a right-angled triangle $\triangle{\text{AOB}}$ with the right angle at O.
To Find:
The coordinates of the point which is equidistant from the three vertices of the triangle.
Solution:
The point which is equidistant from the three vertices of a triangle is called the circumcenter of the triangle.
For a right-angled triangle, the circumcenter is always the midpoint of its hypotenuse.
In $\triangle{\text{AOB}}$, the vertices are O$(0, 0)$, A$(x, 0)$, and B$(0, y)$. The right angle is at O.
The hypotenuse is the side opposite the right angle, which is the line segment AB.
To find the circumcenter, we need to find the midpoint of the hypotenuse AB.
The coordinates of the midpoint of a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ are given by the midpoint formula:
Midpoint $(X, Y) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$
Here, the endpoints of the hypotenuse are A$(x, 0)$ and B$(0, y)$.
Let $(x_1, y_1) = (x, 0)$ and $(x_2, y_2) = (0, y)$.
Calculate the coordinates of the midpoint:
$X = \frac{x + 0}{2} = \frac{x}{2}$
$Y = \frac{0 + y}{2} = \frac{y}{2}$
The coordinates of the circumcenter (the point equidistant from the vertices) are $\left(\frac{x}{2}, \frac{y}{2}\right)$.
Answer:
The coordinates of the point which is equidistant from the three vertices of the $\triangle{\text{AOB}}$ is $\left(\frac{x}{2}, \frac{y}{2}\right)$.
The correct option is (C).
Question 16. A circle drawn with origin as the centre passes through ($\frac{13}{2}$ , 0). The point which does not lie in the interior of the circle is
(A) $\left( \frac{-3}{4} , 1 \right)$
(B) $\left( 2 , \frac{7}{3} \right)$
(C) $\left( 5 , \frac{-1}{2} \right)$
(D) $\left( -6 , \frac{5}{2} \right)$
Answer:
Given:
Centre of the circle is the origin O$(0, 0)$.
The circle passes through the point A$\left(\frac{13}{2}, 0\right)$.
Four points are given in the options.
To Find:
The point which does not lie in the interior of the circle.
Solution:
The radius of the circle is the distance from the centre (origin) to the point it passes through.
Radius, $r$ = Distance between O$(0, 0)$ and A$\left(\frac{13}{2}, 0\right)$.
Using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$:
$r = \sqrt{\left(\frac{13}{2} - 0\right)^2 + (0 - 0)^2}$
$r = \sqrt{\left(\frac{13}{2}\right)^2 + 0^2}$}
$r = \sqrt{\frac{169}{4}}$
$r = \frac{13}{2}$
The equation of the circle with centre $(0, 0)$ and radius $r$ is $x^2 + y^2 = r^2$.
The equation of this circle is $x^2 + y^2 = \left(\frac{13}{2}\right)^2 = \frac{169}{4}$.
A point P$(x, y)$ lies:
In the interior of the circle if $x^2 + y^2 < r^2$, i.e., $x^2 + y^2 < \frac{169}{4}$.
On the circle if $x^2 + y^2 = r^2$, i.e., $x^2 + y^2 = \frac{169}{4}$.
Outside the circle if $x^2 + y^2 > r^2$, i.e., $x^2 + y^2 > \frac{169}{4}$.
We need to find the point for which $x^2 + y^2 \geq \frac{169}{4}$ (since it does not lie in the interior).
Let's check each option:
(A) $\left( \frac{-3}{4} , 1 \right)$
$x^2 + y^2 = \left(\frac{-3}{4}\right)^2 + 1^2 = \frac{9}{16} + 1 = \frac{9 + 16}{16} = \frac{25}{16}$
Compare $\frac{25}{16}$ with $\frac{169}{4}$. $\frac{169}{4} = \frac{169 \times 4}{4 \times 4} = \frac{676}{16}$.
Since $\frac{25}{16} < \frac{676}{16}$, the point is in the interior.
(B) $\left( 2 , \frac{7}{3} \right)$
$x^2 + y^2 = 2^2 + \left(\frac{7}{3}\right)^2 = 4 + \frac{49}{9} = \frac{36 + 49}{9} = \frac{85}{9}$
Compare $\frac{85}{9}$ with $\frac{169}{4}$. $\frac{85}{9} = \frac{85 \times 4}{9 \times 4} = \frac{340}{36}$. $\frac{169}{4} = \frac{169 \times 9}{4 \times 9} = \frac{1521}{36}$.
Since $\frac{340}{36} < \frac{1521}{36}$, the point is in the interior.
(C) $\left( 5 , \frac{-1}{2} \right)$
$x^2 + y^2 = 5^2 + \left(\frac{-1}{2}\right)^2 = 25 + \frac{1}{4} = \frac{100 + 1}{4} = \frac{101}{4}$
Compare $\frac{101}{4}$ with $\frac{169}{4}$.
Since $\frac{101}{4} < \frac{169}{4}$, the point is in the interior.
(D) $\left( -6 , \frac{5}{2} \right)$
$x^2 + y^2 = (-6)^2 + \left(\frac{5}{2}\right)^2 = 36 + \frac{25}{4} = \frac{36 \times 4 + 25}{4} = \frac{144 + 25}{4} = \frac{169}{4}$
Compare $\frac{169}{4}$ with $\frac{169}{4}$.
Since $\frac{169}{4} = \frac{169}{4}$, the point lies on the circle. A point on the circle is not in its interior.
Answer:
The point which does not lie in the interior of the circle is $\left( -6 , \frac{5}{2} \right)$.
The correct option is (D).
Question 17. A line intersects the y-axis and x-axis at the points P and Q, respectively. If (2, –5) is the mid-point of PQ, then the coordinates of P and Q are, respectively
(A) (0, – 5) and (2, 0)
(B) (0, 10) and (– 4, 0)
(C) (0, 4) and (– 10, 0)
(D) (0, – 10) and (4, 0)
Answer:
Given:
A line intersects the y-axis at point P and the x-axis at point Q.
The mid-point of the line segment PQ is $(2, -5)$.
To Find:
The coordinates of points P and Q.
Solution:
Let the coordinates of point P be $(x_1, y_1)$ and the coordinates of point Q be $(x_2, y_2)$.
Since point P lies on the y-axis, its x-coordinate is 0. So, $P = (0, y_1)$.
Since point Q lies on the x-axis, its y-coordinate is 0. So, $Q = (x_2, 0)$.
The mid-point M of the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is given by the mid-point formula:
M $(x_m, y_m) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$
We are given that the mid-point is $(2, -5)$.
So, $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) = (2, -5)$.
Substitute the coordinates of P $(0, y_1)$ and Q $(x_2, 0)$ into the formula:
$\left(\frac{0 + x_2}{2}, \frac{y_1 + 0}{2}\right) = (2, -5)$
$\left(\frac{x_2}{2}, \frac{y_1}{2}\right) = (2, -5)$
Equating the corresponding coordinates:
For the x-coordinate:
$\frac{x_2}{2} = 2$
$x_2 = 2 \times 2$
$x_2 = 4$
For the y-coordinate:
$\frac{y_1}{2} = -5$
$y_1 = -5 \times 2$
$y_1 = -10$
Thus, the coordinates of point P are $(0, y_1) = (0, -10)$.
The coordinates of point Q are $(x_2, 0) = (4, 0)$.
Answer:
The coordinates of P and Q are, respectively, (0, – 10) and (4, 0).
The correct option is (D).
Question 18. The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is
(A) (a + b + c)2
(B) 0
(C) a + b + c
(D) abc
Answer:
Given:
The vertices of the triangle are A$(a, b+c)$, B$(b, c+a)$, and C$(c, a+b)$.
To Find:
The area of the triangle with the given vertices.
Solution:
We can calculate the area of a triangle using the coordinates of its vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ using the formula:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Let $(x_1, y_1) = (a, b+c)$, $(x_2, y_2) = (b, c+a)$, and $(x_3, y_3) = (c, a+b)$.
Calculate the terms inside the absolute value:
$y_2 - y_3 = (c+a) - (a+b) = c+a-a-b = c-b$
$y_3 - y_1 = (a+b) - (b+c) = a+b-b-c = a-c$
$y_1 - y_2 = (b+c) - (c+a) = b+c-c-a = b-a$
Substitute these differences and the x-coordinates into the area formula:
Area $= \frac{1}{2} |a(c-b) + b(a-c) + c(b-a)|$
Area $= \frac{1}{2} |(ac - ab) + (ab - bc) + (bc - ac)|$
Area $= \frac{1}{2} |ac - ab + ab - bc + bc - ac|$
Combine like terms inside the absolute value:
Area $= \frac{1}{2} |(ac - ac) + (-ab + ab) + (-bc + bc)|$
Area $= \frac{1}{2} |0 + 0 + 0|$
Area $= \frac{1}{2} |0|$
Area $= \frac{1}{2} \times 0$
Area $= 0$ square units.
Since the area of the triangle is 0, the three points are collinear (lie on the same straight line).
Answer:
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is $0$.
The correct option is (B).
Question 19. If the distance between the points (4, p) and (1, 0) is 5, then the value of p is
(A) 4 only
(B) ± 4
(C) – 4 only
(D) 0
Answer:
Given:
Two points: $(4, p)$ and $(1, 0)$.
The distance between the points is $5$ units.
To Find:
The value of $p$.}
Solution:
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ in a coordinate plane is given by the distance formula:
$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
Here, let $(x_1, y_1) = (4, p)$ and $(x_2, y_2) = (1, 0)$. The distance $d = 5$.
Substitute the given values into the distance formula:
$5 = \sqrt{(1 - 4)^2 + (0 - p)^2}$
$5 = \sqrt{(-3)^2 + (-p)^2}$}
$5 = \sqrt{9 + p^2}$
To eliminate the square root, square both sides of the equation:
$5^2 = 9 + p^2$
$25 = 9 + p^2$
Subtract 9 from both sides:
$25 - 9 = p^2$
$16 = p^2$
Take the square root of both sides:
$p = \pm \sqrt{16}$
$p = \pm 4$
The possible values for $p$ are $4$ and $-4$. This can be written as $\pm 4$.}
Answer:
The value of $p$ is $\pm 4$.
The correct option is (B).
Question 20. If the points A (1, 2), O (0, 0) and C (a, b) are collinear, then
(A) a = b
(B) a = 2b
(C) 2a = b
(D) a = –b
Answer:
Given:
The three points A $(1, 2)$, O $(0, 0)$, and C $(a, b)$ are collinear.
To Find:
The relationship between $a$ and $b$.}
Solution:
If three points are collinear, the area of the triangle formed by these three points is 0.
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by the formula:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Let $(x_1, y_1) = (1, 2)$, $(x_2, y_2) = (0, 0)$, and $(x_3, y_3) = (a, b)$.
Since the points are collinear, the area of $\triangle{\text{AOC}} = 0$.
$0 = \frac{1}{2} |1(0 - b) + 0(b - 2) + a(2 - 0)|$
$0 = \frac{1}{2} |-b + 0 + 2a|$
$0 = \frac{1}{2} |2a - b|$
Multiply both sides by 2:
$0 = |2a - b|$
This implies that $2a - b = 0$.}
So, $2a = b$.}
Alternate Solution using Slope:
If three points are collinear, the slope between any two pairs of points is the same (provided the line is not vertical).
Slope of line segment AO (joining A$(1, 2)$ and O$(0, 0)$):
$m_{\text{AO}} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{0 - 2}{0 - 1} = \frac{-2}{-1} = 2$
Slope of line segment OC (joining O$(0, 0)$ and C$(a, b)$):
$m_{\text{OC}} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{b - 0}{a - 0} = \frac{b}{a}$} (assuming $a \neq 0$)
For collinearity, the slopes must be equal:
$m_{\text{AO}} = m_{\text{OC}}$
$2 = \frac{b}{a}$
Multiply both sides by $a$:
$2a = b$}
If $a = 0$, the point C is $(0, b)$. The points are A$(1, 2)$, O$(0, 0)$, C$(0, b)$. For these points to be collinear, they must lie on the same vertical line (x=0). But A has x=1, so A is not on the y-axis. Therefore, for collinearity with O and C on the y-axis, A must also be on the y-axis, which is not the case here. Thus, $a$ cannot be 0 if the points are collinear.
Both methods lead to the same condition: $2a = b$.
Answer:
If the points A (1, 2), O (0, 0) and C (a, b) are collinear, then $2a = b$.
The correct option is (C).
Sample Question 1 to 3 (Before Exercise 7.2)
State whether the following statements are true or false. Justify your answer.
Sample Question 1: The points A (–1, 0), B (3, 1), C (2, 2) and D (–2, 1) are the vertices of a parallelogram.
Answer:
Statement:
The points A $(-1, 0)$, B $(3, 1)$, C $(2, 2)$ and D $(-2, 1)$ are the vertices of a parallelogram.
Justification:
A quadrilateral is a parallelogram if and only if its diagonals bisect each other. This means the midpoint of one diagonal is the same as the midpoint of the other diagonal.
Let's find the midpoint of the diagonal AC and the midpoint of the diagonal BD.
The midpoint formula for a line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Midpoint of diagonal AC (joining A$(-1, 0)$ and C$(2, 2)$):
Midpoint of AC $= \left(\frac{-1 + 2}{2}, \frac{0 + 2}{2}\right) = \left(\frac{1}{2}, \frac{2}{2}\right) = \left(\frac{1}{2}, 1\right)$
Midpoint of diagonal BD (joining B$(3, 1)$ and D$(-2, 1)$):
Midpoint of BD $= \left(\frac{3 + (-2)}{2}, \frac{1 + 1}{2}\right) = \left(\frac{3 - 2}{2}, \frac{2}{2}\right) = \left(\frac{1}{2}, 1\right)$
Since the midpoint of AC is the same as the midpoint of BD, the diagonals bisect each other.
Therefore, the points A, B, C, and D are the vertices of a parallelogram.
Answer:
The statement is True.
Sample Question 2: The points (4, 5), (7, 6) and (6, 3) are collinear.
Answer:
Given:
The three points are A$(4, 5)$, B$(7, 6)$, and C$(6, 3)$.
To Check:
Whether the given points are collinear.
Justification:
Three points are collinear if the area of the triangle formed by these points is 0.
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by the formula:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Let $(x_1, y_1) = (4, 5)$, $(x_2, y_2) = (7, 6)$, and $(x_3, y_3) = (6, 3)$.
Substitute the coordinates into the formula:
Area $= \frac{1}{2} |4(6 - 3) + 7(3 - 5) + 6(5 - 6)|$
Area $= \frac{1}{2} |4(3) + 7(-2) + 6(-1)|$
Area $= \frac{1}{2} |12 - 14 - 6|$
Area $= \frac{1}{2} |12 - 20|$
Area $= \frac{1}{2} |-8|$
Area $= \frac{1}{2} \times 8$
Area $= 4$ square units.
Since the area of the triangle formed by the given points is $4$, which is not equal to $0$, the points are not collinear.
Answer:
The statement is False.
Sample Question 3: Point P (0, –7) is the point of intersection of y-axis and perpendicular bisector of line segment joining the points A (–1, 0) and B (7, –6).
Answer:
Statement:
Point P $(0, -7)$ is the point of intersection of y-axis and perpendicular bisector of line segment joining the points A $(-1, 0)$ and B $(7, -6)$.
Justification:
To verify the statement, we need to find the equation of the perpendicular bisector of the line segment joining points A $(-1, 0)$ and B $(7, -6)$ and then find where this perpendicular bisector intersects the y-axis (which is the line with equation $x = 0$).
First, find the midpoint of the line segment AB. The midpoint M of a segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Midpoint of AB, M $= \left(\frac{-1 + 7}{2}, \frac{0 + (-6)}{2}\right) = \left(\frac{6}{2}, \frac{-6}{2}\right) = (3, -3)$.
Next, find the slope of the line segment AB. The slope $m$ of a segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m = \frac{y_2 - y_1}{x_2 - x_1}$.
Slope of AB, $m_{\text{AB}} = \frac{-6 - 0}{7 - (-1)} = \frac{-6}{7 + 1} = \frac{-6}{8} = -\frac{3}{4}$.
The perpendicular bisector is perpendicular to the line segment AB. The slope of a line perpendicular to AB is the negative reciprocal of the slope of AB.
Slope of the perpendicular bisector, $m_{\perp} = -\frac{1}{m_{\text{AB}}} = -\frac{1}{-3/4} = \frac{4}{3}$.
Now, find the equation of the perpendicular bisector. We have the slope $m_{\perp} = \frac{4}{3}$ and it passes through the midpoint M $(3, -3)$. Using the point-slope form $y - y_1 = m(x - x_1)$:
$y - (-3) = \frac{4}{3}(x - 3)$
$y + 3 = \frac{4}{3}x - \frac{4}{3} \times 3$
$y + 3 = \frac{4}{3}x - 4$
$y = \frac{4}{3}x - 4 - 3$
$y = \frac{4}{3}x - 7$
This is the equation of the perpendicular bisector of AB.
To find where this line intersects the y-axis, we set $x = 0$ in the equation:
$y = \frac{4}{3}(0) - 7$
$y = 0 - 7$
$y = -7$
The point of intersection of the perpendicular bisector and the y-axis is $(0, -7)$.
The given point P is $(0, -7)$.
Since the calculated intersection point $(0, -7)$ is the same as the given point P $(0, -7)$, the statement is true.
Answer:
The statement is True.
Exercise 7.2
State whether the following statements are true or false. Justify your answer.
Question 1. Δ ABC with vertices A (–2, 0), B (2, 0) and C (0, 2) is similar to Δ DEF with vertices D (–4, 0) E (4, 0) and F (0, 4).
Answer:
Given:
Vertices of $\triangle{\text{ABC}}$ are A $(-2, 0)$, B $(2, 0)$, and C $(0, 2)$.
Vertices of $\triangle{\text{DEF}}$ are D $(-4, 0)$, E $(4, 0)$, and F $(0, 4)$.
To Check:
Whether $\triangle{\text{ABC}}$ is similar to $\triangle{\text{DEF}}$.
Justification:
To check if the triangles are similar, we can compare the ratios of their corresponding sides (SSS similarity criterion) or compare their angles (AA or AAA similarity criterion). Let's find the lengths of the sides of both triangles using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
For $\triangle{\text{ABC}}$:
Length of AB: $\sqrt{(2 - (-2))^2 + (0 - 0)^2} = \sqrt{(2+2)^2 + 0^2} = \sqrt{4^2} = \sqrt{16} = 4$.
Length of BC: $\sqrt{(0 - 2)^2 + (2 - 0)^2} = \sqrt{(-2)^2 + 2^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$.
Length of AC: $\sqrt{(0 - (-2))^2 + (2 - 0)^2} = \sqrt{(0+2)^2 + 2^2} = \sqrt{2^2 + 2^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$.
The side lengths of $\triangle{\text{ABC}}$ are 4, $2\sqrt{2}$, and $2\sqrt{2}$.
For $\triangle{\text{DEF}}$:
Length of DE: $\sqrt{(4 - (-4))^2 + (0 - 0)^2} = \sqrt{(4+4)^2 + 0^2} = \sqrt{8^2} = \sqrt{64} = 8$.
Length of EF: $\sqrt{(0 - 4)^2 + (4 - 0)^2} = \sqrt{(-4)^2 + 4^2} = \sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2}$.
Length of DF: $\sqrt{(0 - (-4))^2 + (4 - 0)^2} = \sqrt{(0+4)^2 + 4^2} = \sqrt{4^2 + 4^2} = \sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2}$.
The side lengths of $\triangle{\text{DEF}}$ are 8, $4\sqrt{2}$, and $4\sqrt{2}$.
Now, let's check the ratios of corresponding sides. Assuming the correspondence A to D, B to E, and C to F:
Ratio $\frac{\text{AB}}{\text{DE}} = \frac{4}{8} = \frac{1}{2}$.
Ratio $\frac{\text{BC}}{\text{EF}} = \frac{2\sqrt{2}}{4\sqrt{2}} = \frac{2}{4} = \frac{1}{2}$.
Ratio $\frac{\text{AC}}{\text{DF}} = \frac{2\sqrt{2}}{4\sqrt{2}} = \frac{2}{4} = \frac{1}{2}$.
Since the ratios of all corresponding sides are equal ($\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF} = \frac{1}{2}$), the triangles $\triangle{\text{ABC}}$ and $\triangle{\text{DEF}}$ are similar by the SSS similarity criterion.
Answer:
The statement is True.
Question 2. Point P (– 4, 2) lies on the line segment joining the points A (– 4, 6) and B (– 4, – 6).
Answer:
Given:
Point A $= (-4, 6)$.
Point B $= (-4, -6)$.
Point P $= (-4, 2)$.
To Check:
Whether point P lies on the line segment joining A and B.
Justification:
For a point P to lie on the line segment joining points A and B, two conditions must be satisfied:
1. The three points A, P, and B must be collinear.
2. The distance between A and B must be equal to the sum of the distances between A and P, and P and B (i.e., AB = AP + PB).
Let's check the collinearity first. Points A $(-4, 6)$, B $(-4, -6)$, and P $(-4, 2)$ all have the same x-coordinate, which is $-4$. This means all three points lie on the vertical line $x = -4$. Any three points lying on the same straight line are collinear.
So, condition 1 is satisfied.
Now, let's calculate the distances between the points using the distance formula. For points on a vertical line with the same x-coordinate, the distance between $(k, y_1)$ and $(k, y_2)$ is $|y_2 - y_1|$.
Distance AB (between A$(-4, 6)$ and B$(-4, -6)$):
$AB = |-6 - 6| = |-12| = 12$ units.
Distance AP (between A$(-4, 6)$ and P$(-4, 2)$):
$AP = |2 - 6| = |-4| = 4$ units.
Distance PB (between P$(-4, 2)$ and B$(-4, -6)$):
$PB = |-6 - 2| = |-8| = 8$ units.
Now, check if AP + PB = AB:
$AP + PB = 4 + 8 = 12$ units.
Since $AP + PB = 12$ and $AB = 12$, we have $AP + PB = AB$.
This means that point P lies between points A and B on the line segment AB.
Both conditions are satisfied.
Answer:
The statement is True.
Question 3. The points (0, 5), (0, –9) and (3, 6) are collinear.
Answer:
Statement:
The points (0, 5), (0, –9) and (3, 6) are collinear.
Justification:
Let the given points be A$(0, 5)$, B$(0, -9)$, and C$(3, 6)$.
Three points are collinear if and only if the area of the triangle formed by these points is 0.
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by the formula:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Let $(x_1, y_1) = (0, 5)$, $(x_2, y_2) = (0, -9)$, and $(x_3, y_3) = (3, 6)$.
Substitute the coordinates into the formula:
Area $= \frac{1}{2} |0(-9 - 6) + 0(6 - 5) + 3(5 - (-9))|$
Area $= \frac{1}{2} |0(-15) + 0(1) + 3(5 + 9)|$}
Area $= \frac{1}{2} |0 + 0 + 3(14)|$}
Area $= \frac{1}{2} |42|$
Area $= \frac{1}{2} \times 42$
Area $= 21$ square units.
Since the area of the triangle formed by the given points is $21$, which is not equal to $0$, the points are not collinear.
Alternatively, consider the points A$(0, 5)$ and B$(0, -9)$. Both points have an x-coordinate of 0, so they lie on the y-axis. The point C$(3, 6)$ has an x-coordinate of 3, which means it does not lie on the y-axis. Therefore, the three points cannot lie on the same straight line.
Answer:
The statement is False.
Question 4. Point P (0, 2) is the point of intersection of y–axis and perpendicular bisector of line segment joining the points A (–1, 1) and B (3, 3).
Answer:
Statement:
Point P $(0, 2)$ is the point of intersection of y–axis and perpendicular bisector of line segment joining the points A $(-1, 1)$ and B $(3, 3)$.
Justification:
To verify the statement, we need to find the equation of the perpendicular bisector of the line segment joining points A $(-1, 1)$ and B $(3, 3)$ and then find where this perpendicular bisector intersects the y-axis (which is the line with equation $x = 0$).
First, find the midpoint of the line segment AB. The midpoint M of a segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Midpoint of AB, M $= \left(\frac{-1 + 3}{2}, \frac{1 + 3}{2}\right) = \left(\frac{2}{2}, \frac{4}{2}\right) = (1, 2)$.
Next, find the slope of the line segment AB. The slope $m$ of a segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m = \frac{y_2 - y_1}{x_2 - x_1}$.
Slope of AB, $m_{\text{AB}} = \frac{3 - 1}{3 - (-1)} = \frac{2}{3 + 1} = \frac{2}{4} = \frac{1}{2}$.
The perpendicular bisector is perpendicular to the line segment AB. The slope of a line perpendicular to another line with slope $m$ is $-\frac{1}{m}$ (if $m \neq 0$).
Slope of the perpendicular bisector, $m_{\perp} = -\frac{1}{m_{\text{AB}}} = -\frac{1}{1/2} = -2$.
Now, find the equation of the perpendicular bisector. We have the slope $m_{\perp} = -2$ and it passes through the midpoint M $(1, 2)$. Using the point-slope form $y - y_1 = m(x - x_1)$:
$y - 2 = -2(x - 1)$
$y - 2 = -2x + 2$
$y = -2x + 2 + 2$
$y = -2x + 4$
This is the equation of the perpendicular bisector of AB.
To find where this line intersects the y-axis, we set $x = 0$ in the equation:
$y = -2(0) + 4$
$y = 0 + 4$
$y = 4$
The point of intersection of the perpendicular bisector and the y-axis is $(0, 4)$.
The given point P is $(0, 2)$.
Since the calculated intersection point $(0, 4)$ is not the same as the given point P $(0, 2)$, the statement is false.
Answer:
The statement is False.
Question 5. Points A (3, 1), B (12, –2) and C (0, 2) cannot be the vertices of a triangle.
Answer:
Statement:
Points A $(3, 1)$, B $(12, -2)$ and C $(0, 2)$ cannot be the vertices of a triangle.
Justification:
For three given points to be the vertices of a triangle, they must not be collinear. If the three points are collinear, they lie on the same straight line and thus cannot form a triangle.
We can check for collinearity by calculating the area of the triangle formed by the points. If the area is 0, the points are collinear.
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by the formula:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Let $(x_1, y_1) = (3, 1)$, $(x_2, y_2) = (12, -2)$, and $(x_3, y_3) = (0, 2)$.
Substitute the coordinates into the formula:
Area $= \frac{1}{2} |3(-2 - 2) + 12(2 - 1) + 0(1 - (-2))|$
Area $= \frac{1}{2} |3(-4) + 12(1) + 0(3)|$}
Area $= \frac{1}{2} |-12 + 12 + 0|$
Area $= \frac{1}{2} |0|$
Area $= \frac{1}{2} \times 0$
Area $= 0$ square units.
Since the area of the triangle formed by the given points is 0, the points A, B, and C are collinear.
Therefore, the points cannot form the vertices of a triangle.
Answer:
The statement is True.
Question 6. Points A (4, 3), B (6, 4), C (5, –6) and D (–3, 5) are the vertices of a parallelogram.
Answer:
Statement:
Points A $(4, 3)$, B $(6, 4)$, C $(5, -6)$ and D $(-3, 5)$ are the vertices of a parallelogram.
Justification:
A quadrilateral is a parallelogram if and only if its diagonals bisect each other. This means the midpoint of the diagonal AC must be the same as the midpoint of the diagonal BD.
The midpoint of a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the formula $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Let's find the midpoint of the diagonal AC, which joins A$(4, 3)$ and C$(5, -6)$.
Midpoint of AC $= \left(\frac{4 + 5}{2}, \frac{3 + (-6)}{2}\right)$
Midpoint of AC $= \left(\frac{9}{2}, \frac{3 - 6}{2}\right)$
Midpoint of AC $= \left(\frac{9}{2}, \frac{-3}{2}\right)$
Now, let's find the midpoint of the diagonal BD, which joins B$(6, 4)$ and D$(-3, 5)$.
Midpoint of BD $= \left(\frac{6 + (-3)}{2}, \frac{4 + 5}{2}\right)$
Midpoint of BD $= \left(\frac{6 - 3}{2}, \frac{9}{2}\right)$
Midpoint of BD $= \left(\frac{3}{2}, \frac{9}{2}\right)$
The midpoint of diagonal AC is $\left(\frac{9}{2}, \frac{-3}{2}\right)$ and the midpoint of diagonal BD is $\left(\frac{3}{2}, \frac{9}{2}\right)$.
Since the coordinates of the midpoints are not the same, the diagonals AC and BD do not bisect each other.
Therefore, the points A, B, C, and D, in this order, do not form a parallelogram.
Answer:
The statement is False.
Question 7. A circle has its centre at the origin and a point P (5, 0) lies on it. The point Q (6, 8) lies outside the circle.
Answer:
Given:
Centre of the circle is the origin O $(0, 0)$.
A point P $(5, 0)$ lies on the circle.
A point Q $(6, 8)$.
To Check:
Whether the point Q $(6, 8)$ lies outside the circle.
Justification:
The radius of the circle is the distance from the centre to any point on the circle.
Radius $r$ = Distance between O $(0, 0)$ and P $(5, 0)$.
Using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$:
$r = \sqrt{(5 - 0)^2 + (0 - 0)^2}$
$r = \sqrt{5^2 + 0^2}$}
$r = \sqrt{25}$}
$r = 5$ units.
Now, find the distance of point Q $(6, 8)$ from the centre O $(0, 0)$.
Distance OQ = $\sqrt{(6 - 0)^2 + (8 - 0)^2}$}
Distance OQ = $\sqrt{6^2 + 8^2}$}
Distance OQ = $\sqrt{36 + 64}$}
Distance OQ = $\sqrt{100}$}
Distance OQ = $10$ units.
To determine if point Q lies inside, on, or outside the circle, we compare its distance from the centre (OQ) with the radius of the circle (r).
If OQ < r, the point lies inside the circle.
If OQ = r, the point lies on the circle.
If OQ > r, the point lies outside the circle.
In this case, OQ = $10$ units and r = $5$ units.
Since $10 > 5$, we have OQ > r.
Therefore, the point Q $(6, 8)$ lies outside the circle.
The statement says that point Q $(6, 8)$ lies outside the circle, which is consistent with our calculation.
Answer:
The statement is True.
Question 8. The point A (2, 7) lies on the perpendicular bisector of line segment joining the points P (6, 5) and Q (0, – 4).
Answer:
Statement:
The point A $(2, 7)$ lies on the perpendicular bisector of line segment joining the points P $(6, 5)$ and Q $(0, -4)$.
Justification:
A point lies on the perpendicular bisector of a line segment if and only if it is equidistant from the endpoints of the segment.
We need to check if the distance from point A $(2, 7)$ to point P $(6, 5)$ is equal to the distance from point A $(2, 7)$ to point Q $(0, -4)$.
Using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$:
Calculate the distance AP (between A$(2, 7)$ and P$(6, 5)$):
$AP = \sqrt{(6 - 2)^2 + (5 - 7)^2}$}
$AP = \sqrt{(4)^2 + (-2)^2}$}
$AP = \sqrt{16 + 4}$}
$AP = \sqrt{20}$ units.
Calculate the distance AQ (between A$(2, 7)$ and Q$(0, -4)$):
$AQ = \sqrt{(0 - 2)^2 + (-4 - 7)^2}$}
$AQ = \sqrt{(-2)^2 + (-11)^2}$}
$AQ = \sqrt{4 + 121}$}
$AQ = \sqrt{125}$ units.
Compare the distances AP and AQ:
$AP = \sqrt{20}$}
$AQ = \sqrt{125}$}
Since $\sqrt{20} \neq \sqrt{125}$, the distance AP is not equal to the distance AQ.
Since point A is not equidistant from points P and Q, it does not lie on the perpendicular bisector of the line segment PQ.
Answer:
The statement is False.
Question 9. Point P (5, –3) is one of the two points of trisection of the line segment joining the points A (7, – 2) and B (1, – 5).
Answer:
Statement:
Point P $(5, -3)$ is one of the two points of trisection of the line segment joining the points A $(7, -2)$ and B $(1, -5)$.
Given:
Point A $= (7, -2)$.
Point B $= (1, -5)$.
Point P $= (5, -3)$.
To Check:
Whether point P is one of the two points of trisection of line segment AB.
Justification:
The points of trisection divide the line segment into three equal parts. Let the two points of trisection be T$_1$ and T$_2$. If T$_1$ and T$_2$ are the points such that A, T$_1$, T$_2$, B are in order on the line segment, then T$_1$ divides AB in the ratio $1:2$, and T$_2$ divides AB in the ratio $2:1$.}
We can use the section formula to find the coordinates of these points. The coordinates of a point $(x, y)$ dividing the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ internally in the ratio $m:n$ are given by:
$x = \frac{m x_2 + n x_1}{m+n}$
$y = \frac{m y_2 + n y_1}{m+n}$
Let's find the coordinates of the point that divides AB in the ratio $1:2$.}
Here, $(x_1, y_1) = (7, -2)$, $(x_2, y_2) = (1, -5)$, $m = 1$, and $n = 2$.
x-coordinate: $x = \frac{1(1) + 2(7)}{1+2} = \frac{1 + 14}{3} = \frac{15}{3} = 5$}
y-coordinate: $y = \frac{1(-5) + 2(-2)}{1+2} = \frac{-5 - 4}{3} = \frac{-9}{3} = -3$}
The coordinates of the point dividing AB in the ratio $1:2$ are $(5, -3)$.
This calculated point $(5, -3)$ is exactly the given point P $(5, -3)$.
So, P is one of the points of trisection (specifically, the one closer to point A).
We can also calculate the coordinates of the point that divides AB in the ratio $2:1$ to find the other point of trisection.
Here, $m = 2$, and $n = 1$.}
x-coordinate: $x = \frac{2(1) + 1(7)}{2+1} = \frac{2 + 7}{3} = \frac{9}{3} = 3$}
y-coordinate: $y = \frac{2(-5) + 1(-2)}{2+1} = \frac{-10 - 2}{3} = \frac{-12}{3} = -4$}
The coordinates of the other point of trisection are $(3, -4)$.
The two points of trisection of the line segment joining A $(7, -2)$ and B $(1, -5)$ are $(5, -3)$ and $(3, -4)$.
The given point P $(5, -3)$ is one of these two points.
Answer:
The statement is True.
Question 10. Points A (–6, 10), B (–4, 6) and C (3, –8) are collinear such that AB = $\frac{2}{9}$ AC .
Answer:
Statement:
Points A $(-6, 10)$, B $(-4, 6)$ and C $(3, -8)$ are collinear such that AB = $\frac{2}{9}$ AC.
Given:
Point A $= (-6, 10)$.
Point B $= (-4, 6)$.
Point C $= (3, -8)$.
To Check:
1. Whether the points A, B, and C are collinear.
2. If they are collinear, whether the relationship AB = $\frac{2}{9}$ AC holds.
Justification:
To check for collinearity, we can calculate the slopes of the line segments AB and BC. If the slopes are equal, the points A, B, and C are collinear.
The slope of a line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is $m = \frac{y_2 - y_1}{x_2 - x_1}$.
Slope of AB ($m_{\text{AB}}$):
$m_{\text{AB}} = \frac{6 - 10}{-4 - (-6)} = \frac{-4}{-4 + 6} = \frac{-4}{2} = -2$
Slope of BC ($m_{\text{BC}}$):
$m_{\text{BC}} = \frac{-8 - 6}{3 - (-4)} = \frac{-14}{3 + 4} = \frac{-14}{7} = -2$
Since the slope of AB is equal to the slope of BC ($m_{\text{AB}} = m_{\text{BC}} = -2$), the points A, B, and C are collinear.
Now that we know the points are collinear, we need to check the distance relationship AB = $\frac{2}{9}$ AC. We will calculate the lengths of the line segments AB and AC using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Length of AB:
$AB = \sqrt{(-4 - (-6))^2 + (6 - 10)^2} = \sqrt{(2)^2 + (-4)^2} = \sqrt{4 + 16} = \sqrt{20}$
Simplify $\sqrt{20}$: $\sqrt{20} = \sqrt{4 \times 5} = \sqrt{4} \times \sqrt{5} = 2\sqrt{5}$.
So, AB = $2\sqrt{5}$ units.
Length of AC:
$AC = \sqrt{(3 - (-6))^2 + (-8 - 10)^2} = \sqrt{(3 + 6)^2 + (-18)^2} = \sqrt{9^2 + 324} = \sqrt{81 + 324} = \sqrt{405}$.
Simplify $\sqrt{405}$: $\sqrt{405} = \sqrt{81 \times 5} = \sqrt{81} \times \sqrt{5} = 9\sqrt{5}$.
So, AC = $9\sqrt{5}$ units.
Now, check if $AB = \frac{2}{9} AC$:
Left side: AB = $2\sqrt{5}$.
Right side: $\frac{2}{9} AC = \frac{2}{9} (9\sqrt{5})$.
$\frac{2}{9} (9\sqrt{5}) = \frac{2}{\cancel{9}} \times \cancel{9}\sqrt{5} = 2\sqrt{5}$.
Since $AB = 2\sqrt{5}$ and $\frac{2}{9} AC = 2\sqrt{5}$, the relationship AB = $\frac{2}{9}$ AC holds true.
Both conditions (collinearity and the distance relationship) are satisfied.
Answer:
The statement is True.
Question 11. The point P (–2, 4) lies on a circle of radius 6 and centre C (3, 5).
Answer:
Statement:
The point P $(-2, 4)$ lies on a circle of radius $6$ and centre C $(3, 5)$.
Given:
Centre of the circle C $= (3, 5)$.
Radius of the circle $r = 6$.
Point P $= (-2, 4)$.
To Check:
Whether point P lies on the circle.
Justification:
A point P$(x, y)$ lies on a circle with centre C$(h, k)$ and radius $r$ if and only if the distance between the point P and the centre C is equal to the radius $r$. That is, $CP = r$.}
We calculate the distance between the point P $(-2, 4)$ and the centre C $(3, 5)$ using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Let $(x_1, y_1) = (3, 5)$ and $(x_2, y_2) = (-2, 4)$.
Distance CP = $\sqrt{(-2 - 3)^2 + (4 - 5)^2}$}
Distance CP = $\sqrt{(-5)^2 + (-1)^2}$}
Distance CP = $\sqrt{25 + 1}$}
Distance CP = $\sqrt{26}$ units.
The given radius of the circle is $r = 6$.}
Now, we compare the distance CP with the radius $r$.
CP $= \sqrt{26}$.
$r = 6$.}
We can compare their squares to make the comparison easier:
$CP^2 = (\sqrt{26})^2 = 26$}
$r^2 = 6^2 = 36$}
Since $26 \neq 36$, we have $CP^2 \neq r^2$, which means $CP \neq r$.}
Specifically, since $26 < 36$, we have $CP^2 < r^2$, which means $CP < r$.}
A point lies on the circle if $CP = r$. Since $CP \neq r$, the point P $(-2, 4)$ does not lie on the circle.
Since $CP < r$, the point P $(-2, 4)$ lies in the interior of the circle.
Therefore, the statement that point P lies on the circle is false.
Answer:
The statement is False.
Question 12. The points A (–1, –2), B (4, 3), C (2, 5) and D (–3, 0) in that order form a rectangle.
Answer:
Statement:
The points A $(-1, -2)$, B $(4, 3)$, C $(2, 5)$ and D $(-3, 0)$ in that order form a rectangle.
Justification:
To determine if the given points form a rectangle, we can check if the opposite sides are equal and if the diagonals are equal. Alternatively, we can check if it is a parallelogram (diagonals bisect each other) and if the diagonals are equal.
Let's calculate the lengths of the sides and the diagonals using the distance formula $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$.
Length of side AB (between A$(-1, -2)$ and B$(4, 3)$):
$AB = \sqrt{(4 - (-1))^2 + (3 - (-2))^2} = \sqrt{(4+1)^2 + (3+2)^2} = \sqrt{5^2 + 5^2} = \sqrt{25 + 25} = \sqrt{50} = 5\sqrt{2}$ units.
Length of side BC (between B$(4, 3)$ and C$(2, 5)$):
$BC = \sqrt{(2 - 4)^2 + (5 - 3)^2} = \sqrt{(-2)^2 + 2^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$ units.
Length of side CD (between C$(2, 5)$ and D$(-3, 0)$):
$CD = \sqrt{(-3 - 2)^2 + (0 - 5)^2} = \sqrt{(-5)^2 + (-5)^2} = \sqrt{25 + 25} = \sqrt{50} = 5\sqrt{2}$ units.
Length of side DA (between D$(-3, 0)$ and A$(-1, -2)$):
$DA = \sqrt{(-1 - (-3))^2 + (-2 - 0)^2} = \sqrt{(-1+3)^2 + (-2)^2} = \sqrt{2^2 + (-2)^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$ units.
Comparing opposite sides: AB = $5\sqrt{2}$ and CD = $5\sqrt{2}$ (AB = CD). BC = $2\sqrt{2}$ and DA = $2\sqrt{2}$ (BC = DA). Since opposite sides are equal in length, the quadrilateral ABCD is a parallelogram.
Now, calculate the lengths of the diagonals AC and BD.
Length of diagonal AC (between A$(-1, -2)$ and C$(2, 5)$):
$AC = \sqrt{(2 - (-1))^2 + (5 - (-2))^2} = \sqrt{(2+1)^2 + (5+2)^2} = \sqrt{3^2 + 7^2} = \sqrt{9 + 49} = \sqrt{58}$ units.
Length of diagonal BD (between B$(4, 3)$ and D$(-3, 0)$):
$BD = \sqrt{(-3 - 4)^2 + (0 - 3)^2} = \sqrt{(-7)^2 + (-3)^2} = \sqrt{49 + 9} = \sqrt{58}$ units.
Comparing the diagonals: AC = $\sqrt{58}$ and BD = $\sqrt{58}$ (AC = BD). Since the diagonals are equal in length, the parallelogram ABCD is a rectangle.
(A parallelogram with equal diagonals is a rectangle).
Answer:
The statement is True.
Sample Question 1 to 4 (Before Exercise 7.3)
Sample Question 1: If the mid-point of the line segment joining the points A (3, 4) and B (k, 6) is P (x, y) and x + y – 10 = 0, find the value of k.
Answer:
Given:
The points A (3, 4) and B (k, 6).
The mid-point of AB is P (x, y).
The coordinates of P (x, y) satisfy the equation $x + y - 10 = 0$.
To Find:
The value of k.
Solution:
Let the coordinates of point A be $(x_1, y_1) = (3, 4)$.
Let the coordinates of point B be $(x_2, y_2) = (k, 6)$.
Let the coordinates of the mid-point P be $(x, y)$.
The formula for the mid-point of a line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)$.
Using the mid-point formula, the coordinates of P are:
$x = \frac{3 + k}{2}$
$y = \frac{4 + 6}{2} = \frac{10}{2} = 5$
So, the coordinates of the mid-point are P $\left(\frac{3+k}{2}, 5\right)$.
We are given that the point P (x, y) satisfies the equation $x + y - 10 = 0$.
Substitute the values of x and y from the mid-point coordinates into this equation.
$\left(\frac{3+k}{2}\right) + 5 - 10 = 0$
... (1)
Simplify the equation:
$\frac{3+k}{2} - 5 = 0$
Add 5 to both sides:
$\frac{3+k}{2} = 5$
Multiply both sides by 2:
$3+k = 5 \times 2$
$3+k = 10$
Subtract 3 from both sides:
$k = 10 - 3$
$k = 7$
Thus, the value of k is 7.
Sample Question 2: Find the area of the triangle ABC with A (1, –4) and the mid-points of sides through A being (2, – 1) and (0, – 1).
Answer:
Given:
Vertex A is (1, –4).
The mid-points of the sides through A (let's call them AB and AC) are D (2, –1) and E (0, –1).
To Find:
The area of triangle ABC.
Solution:
Let the vertices of the triangle be A$(x_1, y_1)$, B$(x_2, y_2)$, and C$(x_3, y_3)$.
We are given A$(1, -4)$, so $(x_1, y_1) = (1, -4)$.
Let D (2, –1) be the mid-point of side AB, and E (0, –1) be the mid-point of side AC.
Using the mid-point formula, the coordinates of the mid-point of a line segment joining $(x_a, y_a)$ and $(x_b, y_b)$ are $\left(\frac{x_a+x_b}{2}, \frac{y_a+y_b}{2}\right)$.
For the mid-point D (2, –1) of AB:
$\frac{x_1+x_2}{2} = 2 \implies \frac{1+x_2}{2} = 2$
$1 + x_2 = 2 \times 2$
$1 + x_2 = 4$
$x_2 = 4 - 1 = 3$
$\frac{y_1+y_2}{2} = -1 \implies \frac{-4+y_2}{2} = -1$
$-4 + y_2 = -1 \times 2$
$-4 + y_2 = -2$
$y_2 = -2 + 4 = 2$
So, the coordinates of vertex B are $(3, 2)$.
For the mid-point E (0, –1) of AC:
$\frac{x_1+x_3}{2} = 0 \implies \frac{1+x_3}{2} = 0$
$1 + x_3 = 0 \times 2$
$1 + x_3 = 0$
$x_3 = 0 - 1 = -1$
$\frac{y_1+y_3}{2} = -1 \implies \frac{-4+y_3}{2} = -1$
$-4 + y_3 = -1 \times 2$
$-4 + y_3 = -2$
$y_3 = -2 + 4 = 2$
So, the coordinates of vertex C are $(-1, 2)$.
The vertices of triangle ABC are A(1, –4), B(3, 2), and C(–1, 2).
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by the formula:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Substitute the coordinates A(1, –4), B(3, 2), C(–1, 2):
$x_1 = 1, y_1 = -4$
$x_2 = 3, y_2 = 2$
$x_3 = -1, y_3 = 2$
Area $= \frac{1}{2} |1(2 - 2) + 3(2 - (-4)) + (-1)(-4 - 2)|$
Area $= \frac{1}{2} |1(0) + 3(2 + 4) + (-1)(-6)|$
Area $= \frac{1}{2} |0 + 3(6) + 6|$
Area $= \frac{1}{2} |0 + 18 + 6|$
Area $= \frac{1}{2} |24|$
Area $= \frac{1}{2} \times 24$
Area $= 12$ square units.
Alternatively, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and half its length. The triangle formed by connecting the midpoints of the sides of a triangle has an area that is one-fourth the area of the original triangle.
Let D (2, -1) and E (0, -1) be the mid-points of AB and AC respectively.
The area of triangle ADE can be calculated using the coordinates A(1, -4), D(2, -1), and E(0, -1).
Area of ADE $= \frac{1}{2} |1(-1 - (-1)) + 2(-1 - (-4)) + 0(-4 - (-1))|$
Area of ADE $= \frac{1}{2} |1(0) + 2(3) + 0(-3)|$
Area of ADE $= \frac{1}{2} |6| = 3$ square units.
Since Area(ABC) $= 4 \times$ Area(ADE),
Area(ABC) $= 4 \times 3 = 12$ square units.
The area of triangle ABC is 12 square units.
Sample Question 3: Name the type of triangle PQR formed by the points P $(\sqrt{2},\sqrt{2})$ , Q $(-\sqrt{2},-\sqrt{2})$ and R $(-\sqrt{6},\sqrt{6})$ .
Answer:
Given:
The points P $(\sqrt{2}, \sqrt{2})$, Q $(-\sqrt{2}, -\sqrt{2})$, and R $(-\sqrt{6}, \sqrt{6})$.
To Find:
The type of triangle PQR.
Solution:
We will find the length of each side of the triangle PQR using the distance formula.
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Let's calculate the squared length of the side PQ:
$PQ^2 = (-\sqrt{2} - \sqrt{2})^2 + (-\sqrt{2} - \sqrt{2})^2$
$PQ^2 = (-2\sqrt{2})^2 + (-2\sqrt{2})^2$
$PQ^2 = (4 \times 2) + (4 \times 2)$
$PQ^2 = 8 + 8$
$PQ^2 = 16$
$PQ = \sqrt{16} = 4$
Let's calculate the squared length of the side QR:
$QR^2 = (-\sqrt{6} - (-\sqrt{2}))^2 + (\sqrt{6} - (-\sqrt{2}))^2$
$QR^2 = (-\sqrt{6} + \sqrt{2})^2 + (\sqrt{6} + \sqrt{2})^2$
$QR^2 = ((\sqrt{2})^2 - 2\sqrt{2}\sqrt{6} + (\sqrt{6})^2) + ((\sqrt{6})^2 + 2\sqrt{6}\sqrt{2} + (\sqrt{2})^2)$
$QR^2 = (2 - 2\sqrt{12} + 6) + (6 + 2\sqrt{12} + 2)$
$QR^2 = (8 - 2\sqrt{12}) + (8 + 2\sqrt{12})$
$QR^2 = 8 + 8$
$QR^2 = 16$
$QR = \sqrt{16} = 4$
Let's calculate the squared length of the side RP:
$RP^2 = (\sqrt{2} - (-\sqrt{6}))^2 + (\sqrt{2} - \sqrt{6})^2$
$RP^2 = (\sqrt{2} + \sqrt{6})^2 + (\sqrt{2} - \sqrt{6})^2$
$RP^2 = ((\sqrt{2})^2 + 2\sqrt{2}\sqrt{6} + (\sqrt{6})^2) + ((\sqrt{2})^2 - 2\sqrt{2}\sqrt{6} + (\sqrt{6})^2)$
$RP^2 = (2 + 2\sqrt{12} + 6) + (2 - 2\sqrt{12} + 6)$
$RP^2 = (8 + 2\sqrt{12}) + (8 - 2\sqrt{12})$
$RP^2 = 8 + 8$
$RP^2 = 16$
$RP = \sqrt{16} = 4$
Comparing the lengths of the sides, we find that:
$PQ = 4$
$QR = 4$
$RP = 4$
Since all three sides of the triangle PQR are equal in length ($PQ = QR = RP$), the triangle PQR is an equilateral triangle.
The type of triangle PQR is equilateral.
Sample Question 4: ABCD is a parallelogram with vertices A (x1 , y1 ), B (x2 , y2 ) and C (x3 , y3 ). Find the coordinates of the fourth vertex D in terms of x1 , x2, x3 , y1 , y2 and y3
Answer:
Given:
The vertices of parallelogram ABCD are A $(x_1, y_1)$, B $(x_2, y_2)$, and C $(x_3, y_3)$.
To Find:
The coordinates of the fourth vertex D $(x_4, y_4)$ in terms of $x_1, x_2, x_3, y_1, y_2, y_3$.
Solution:
In a parallelogram, the diagonals bisect each other. This means that the mid-point of the diagonal AC is the same as the mid-point of the diagonal BD.
Let the coordinates of the fourth vertex D be $(x_4, y_4)$.
Using the mid-point formula, the coordinates of the mid-point of AC are:
Mid-point of AC $= \left(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}\right)$
Using the mid-point formula, the coordinates of the mid-point of BD are:
Mid-point of BD $= \left(\frac{x_2+x_4}{2}, \frac{y_2+y_4}{2}\right)$
Since the mid-points are the same, we can equate the x-coordinates and the y-coordinates:
Equating the x-coordinates:
$\frac{x_1+x_3}{2} = \frac{x_2+x_4}{2}$
... (1)
Equating the y-coordinates:
$\frac{y_1+y_3}{2} = \frac{y_2+y_4}{2}$
... (2)
From equation (1):
$x_1 + x_3 = x_2 + x_4$
To find $x_4$, rearrange the equation:
$x_4 = x_1 + x_3 - x_2$
From equation (2):
$y_1 + y_3 = y_2 + y_4$
To find $y_4$, rearrange the equation:
$y_4 = y_1 + y_3 - y_2$
Thus, the coordinates of the fourth vertex D are $(x_1 + x_3 - x_2, y_1 + y_3 - y_2)$.
Exercise 7.3
Question 1. Name the type of triangle formed by the points A (–5, 6), B (–4, –2) and C (7, 5).
Answer:
Given:
The points A (–5, 6), B (–4, –2), and C (7, 5).
To Find:
The type of triangle formed by these points.
Solution:
We will find the length of each side of the triangle ABC using the distance formula.
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Let's calculate the squared length of the side AB:
$A = (-5, 6)$, $B = (-4, -2)$
$AB^2 = (-4 - (-5))^2 + (-2 - 6)^2$
$AB^2 = (-4 + 5)^2 + (-8)^2$
$AB^2 = (1)^2 + 64$
$AB^2 = 1 + 64 = 65$
$AB = \sqrt{65}$
Let's calculate the squared length of the side BC:
$B = (-4, -2)$, $C = (7, 5)$
$BC^2 = (7 - (-4))^2 + (5 - (-2))^2$
$BC^2 = (7 + 4)^2 + (5 + 2)^2$
$BC^2 = (11)^2 + (7)^2$
$BC^2 = 121 + 49 = 170$
$BC = \sqrt{170}$
Let's calculate the squared length of the side CA:
$C = (7, 5)$, $A = (-5, 6)$
$CA^2 = (-5 - 7)^2 + (6 - 5)^2$
$CA^2 = (-12)^2 + (1)^2$
$CA^2 = 144 + 1 = 145$
$CA = \sqrt{145}$
Comparing the lengths of the sides, we have:
$AB = \sqrt{65}$
$BC = \sqrt{170}$
$CA = \sqrt{145}$
Since $AB \neq BC$, $BC \neq CA$, and $CA \neq AB$, all three sides have different lengths. This means the triangle is a scalene triangle.
Now, let's check if it's a right-angled triangle using the Pythagorean theorem ($a^2 + b^2 = c^2$). We compare the square of the longest side with the sum of the squares of the other two sides.
The squared lengths are $AB^2 = 65$, $BC^2 = 170$, and $CA^2 = 145$. The longest side squared is $BC^2 = 170$.
Sum of squares of the other two sides: $AB^2 + CA^2 = 65 + 145 = 210$.
Since $AB^2 + CA^2 = 210$ and $BC^2 = 170$, we have $AB^2 + CA^2 \neq BC^2$.
Let's check other combinations:
$AB^2 + BC^2 = 65 + 170 = 235 \neq 145 (CA^2)$
$CA^2 + BC^2 = 145 + 170 = 315 \neq 65 (AB^2)$
Since the sum of the squares of any two sides is not equal to the square of the third side, the triangle is not a right-angled triangle.
Since the triangle has all sides of different lengths and is not a right-angled triangle, the type of triangle is a scalene triangle.
Question 2. Find the points on the x–axis which are at a distance of 2$\sqrt{5}$ from the point (7, –4). How many such points are there?
Answer:
Given:
A point P (7, –4).
A set of points on the x-axis at a distance of $2\sqrt{5}$ from P.
To Find:
The coordinates of the points on the x-axis and the number of such points.
Solution:
Let the point on the x-axis be Q. Any point on the x-axis has its y-coordinate equal to 0. So, let the coordinates of the point Q be $(x, 0)$.
The given point is P (7, –4).
The distance between Q$(x, 0)$ and P$(7, -4)$ is given as $2\sqrt{5}$.
Using the distance formula, the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Here, $(x_1, y_1) = (x, 0)$ and $(x_2, y_2) = (7, -4)$.
The distance PQ is $2\sqrt{5}$.
$PQ = \sqrt{(7 - x)^2 + (-4 - 0)^2}$
... (1)
Substitute the given distance into the equation:
$2\sqrt{5} = \sqrt{(7 - x)^2 + (-4)^2}$
Squaring both sides of the equation to eliminate the square root:
$(2\sqrt{5})^2 = (7 - x)^2 + (-4)^2$
$4 \times 5 = (7 - x)^2 + 16$
$20 = (7 - x)^2 + 16$
Subtract 16 from both sides:
$20 - 16 = (7 - x)^2$
$4 = (7 - x)^2$
Taking the square root of both sides:
$\pm\sqrt{4} = 7 - x$
$\pm 2 = 7 - x$
This gives us two possible cases:
Case 1: $2 = 7 - x$
Rearranging the equation to solve for x:
$x = 7 - 2$
$x = 5$
The point on the x-axis is $(5, 0)$.
Case 2: $-2 = 7 - x$
Rearranging the equation to solve for x:
$x = 7 - (-2)$
$x = 7 + 2$
$x = 9$
The point on the x-axis is $(9, 0)$.
The points on the x-axis at a distance of $2\sqrt{5}$ from (7, –4) are (5, 0) and (9, 0).
There are two such points.
Question 3. What type of a quadrilateral do the points A (2, –2), B (7, 3), C (11, –1) and D (6, –6) taken in that order, form?
Answer:
Given:
The points A (2, –2), B (7, 3), C (11, –1), and D (6, –6).
To Find:
The type of quadrilateral formed by these points taken in order.
Solution:
We will find the length of each side and each diagonal of the quadrilateral ABCD using the distance formula.
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Let's calculate the squared length of the side AB:
$A = (2, -2)$, $B = (7, 3)$
$AB^2 = (7 - 2)^2 + (3 - (-2))^2$
$AB^2 = (5)^2 + (3 + 2)^2$
$AB^2 = 5^2 + 5^2$
$AB^2 = 25 + 25 = 50$
$AB = \sqrt{50}$
Let's calculate the squared length of the side BC:
$B = (7, 3)$, $C = (11, -1)$
$BC^2 = (11 - 7)^2 + (-1 - 3)^2$
$BC^2 = (4)^2 + (-4)^2$
$BC^2 = 16 + 16 = 32$
$BC = \sqrt{32}$
Let's calculate the squared length of the side CD:
$C = (11, -1)$, $D = (6, -6)$
$CD^2 = (6 - 11)^2 + (-6 - (-1))^2$
$CD^2 = (-5)^2 + (-6 + 1)^2$
$CD^2 = (-5)^2 + (-5)^2$
$CD^2 = 25 + 25 = 50$
$CD = \sqrt{50}$
Let's calculate the squared length of the side DA:
$D = (6, -6)$, $A = (2, -2)$
$DA^2 = (2 - 6)^2 + (-2 - (-6))^2$
$DA^2 = (-4)^2 + (-2 + 6)^2$
$DA^2 = (-4)^2 + (4)^2$
$DA^2 = 16 + 16 = 32$
$DA = \sqrt{32}$
Comparing the side lengths:
$AB = \sqrt{50}$
$BC = \sqrt{32}$
$CD = \sqrt{50}$
$DA = \sqrt{32}$
We observe that $AB = CD$ and $BC = DA$. The opposite sides of the quadrilateral are equal in length. This means ABCD is a parallelogram.
Now, let's calculate the squared lengths of the diagonals AC and BD.
Let's calculate the squared length of the diagonal AC:
$A = (2, -2)$, $C = (11, -1)$
$AC^2 = (11 - 2)^2 + (-1 - (-2))^2$
$AC^2 = (9)^2 + (-1 + 2)^2$
$AC^2 = 9^2 + 1^2$
$AC^2 = 81 + 1 = 82$
$AC = \sqrt{82}$
Let's calculate the squared length of the diagonal BD:
$B = (7, 3)$, $D = (6, -6)$
$BD^2 = (6 - 7)^2 + (-6 - 3)^2$
$BD^2 = (-1)^2 + (-9)^2$
$BD^2 = 1 + 81 = 82$
$BD = \sqrt{82}$
Comparing the diagonal lengths:
$AC = \sqrt{82}$
$BD = \sqrt{82}$
We observe that $AC = BD$. The diagonals of the quadrilateral are equal in length.
Since the opposite sides are equal and the diagonals are also equal, the quadrilateral ABCD is a **rectangle**.
Question 4. Find the value of a , if the distance between the points A (–3, –14) and B (a, –5) is 9 units.
Answer:
Given:
Point A (–3, –14).
Point B (a, –5).
The distance between points A and B is 9 units.
To Find:
The value of a.
Solution:
Let the coordinates of point A be $(x_1, y_1) = (-3, -14)$.
Let the coordinates of point B be $(x_2, y_2) = (a, -5)$.
The distance between A and B is given as AB = 9.
Using the distance formula, the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
So, the distance AB is:
$AB = \sqrt{(a - (-3))^2 + (-5 - (-14))^2}$
$AB = \sqrt{(a + 3)^2 + (-5 + 14)^2}$
$AB = \sqrt{(a + 3)^2 + (9)^2}$
$AB = \sqrt{(a + 3)^2 + 81}$
We are given that the distance AB is 9 units. So, we can set up the equation:
$\sqrt{(a + 3)^2 + 81} = 9$
... (1)
To eliminate the square root, square both sides of the equation:
$\left(\sqrt{(a + 3)^2 + 81}\right)^2 = 9^2$
$(a + 3)^2 + 81 = 81$
Subtract 81 from both sides of the equation:
$(a + 3)^2 = 81 - 81$
$(a + 3)^2 = 0$
Take the square root of both sides:
$a + 3 = \sqrt{0}$
$a + 3 = 0$
Subtract 3 from both sides to solve for a:
$a = 0 - 3$
$a = -3$
In this specific case, squaring leads to only one possible value for the expression $(a+3)^2=0$, which means $a+3=0$ has only one solution. Therefore, there is only one value for a.
The value of a is -3.
Question 5. Find a point which is equidistant from the points A (–5, 4) and B (–1, 6)? How many such points are there?
Answer:
Given:
Point A (–5, 4).
Point B (–1, 6).
To Find:
A point equidistant from A and B, and the number of such points.
Solution:
Let P $(x, y)$ be a point that is equidistant from points A (–5, 4) and B (–1, 6).
According to the problem statement, the distance from P to A is equal to the distance from P to B.
$PA = PB$
Squaring both sides of the equation, we get:
$PA^2 = PB^2$
We use the distance formula squared: $(x_2 - x_1)^2 + (y_2 - y_1)^2$.
Calculate $PA^2$ using points P$(x, y)$ and A$(-5, 4)$:
$PA^2 = (x - (-5))^2 + (y - 4)^2$
$PA^2 = (x + 5)^2 + (y - 4)^2$
$PA^2 = (x^2 + 10x + 25) + (y^2 - 8y + 16)$
$PA^2 = x^2 + y^2 + 10x - 8y + 41$
Calculate $PB^2$ using points P$(x, y)$ and B$(-1, 6)$:
$PB^2 = (x - (-1))^2 + (y - 6)^2$
$PB^2 = (x + 1)^2 + (y - 6)^2$
$PB^2 = (x^2 + 2x + 1) + (y^2 - 12y + 36)$
$PB^2 = x^2 + y^2 + 2x - 12y + 37$
Equate $PA^2$ and $PB^2$ since P is equidistant from A and B:
$x^2 + y^2 + 10x - 8y + 41 = x^2 + y^2 + 2x - 12y + 37$
Subtract $x^2 + y^2$ from both sides of the equation:
$10x - 8y + 41 = 2x - 12y + 37$
Move all terms to one side to simplify:
$10x - 2x - 8y + 12y + 41 - 37 = 0$
$8x + 4y + 4 = 0$
Divide the entire equation by 4:
$2x + y + 1 = 0$
... (1)
This linear equation represents the relationship between the coordinates $(x, y)$ of any point that is equidistant from A and B. The locus of such points is the perpendicular bisector of the line segment AB.
Any point $(x, y)$ that satisfies the equation $2x + y + 1 = 0$ is equidistant from points A and B.
To find "a" point, we can choose any convenient value for either x or y and solve for the other variable using the equation $2x + y + 1 = 0$.
Let's choose $x = 0$:
$2(0) + y + 1 = 0$
$0 + y + 1 = 0$
$y = -1$
So, the point (0, -1) is one such point that is equidistant from A and B.
(Any point $(x, y)$ such that $y = -2x - 1$ is equidistant from A and B).
Since the set of all points equidistant from two distinct points forms a straight line (the perpendicular bisector), and a straight line contains infinitely many points, there are infinitely many such points.
A point equidistant from A and B can be any point $(x, y)$ satisfying $2x + y + 1 = 0$. One example is (0, -1).
There are infinitely many such points.
Question 6. Find the coordinates of the point Q on the x–axis which lies on the perpendicular bisector of the line segment joining the points A (–5, –2) and B(4, –2). Name the type of triangle formed by the points Q, A and B.
Answer:
Given:
Point A (–5, –2).
Point B (4, –2).
Point Q lies on the x-axis and is on the perpendicular bisector of the line segment AB.
To Find:
The coordinates of point Q.
The type of triangle formed by points Q, A, and B.
Solution:
Let the coordinates of point Q on the x-axis be $(x, 0)$.
Since Q lies on the perpendicular bisector of the line segment AB, Q is equidistant from points A and B.
$QA = QB$
Squaring both sides, we get $QA^2 = QB^2$.
Using the distance formula squared, $(x_2 - x_1)^2 + (y_2 - y_1)^2$:
Calculate $QA^2$ using points Q$(x, 0)$ and A$(-5, -2)$:
$QA^2 = (x - (-5))^2 + (0 - (-2))^2$
$QA^2 = (x + 5)^2 + (0 + 2)^2$
$QA^2 = (x + 5)^2 + 2^2$
$QA^2 = x^2 + 10x + 25 + 4$
$QA^2 = x^2 + 10x + 29$
Calculate $QB^2$ using points Q$(x, 0)$ and B$(4, -2)$:
$QB^2 = (x - 4)^2 + (0 - (-2))^2$
$QB^2 = (x - 4)^2 + (0 + 2)^2$
$QB^2 = (x - 4)^2 + 2^2$
$QB^2 = x^2 - 8x + 16 + 4$
$QB^2 = x^2 - 8x + 20$
Equate $QA^2$ and $QB^2$ since Q is equidistant from A and B:
$x^2 + 10x + 29 = x^2 - 8x + 20$
... (1)
Subtract $x^2$ from both sides:
$10x + 29 = -8x + 20$
Add 8x to both sides:
$10x + 8x + 29 = 20$
$18x + 29 = 20$
Subtract 29 from both sides:
$18x = 20 - 29$
$18x = -9$
Divide by 18:
$x = \frac{-9}{18} = -\frac{1}{2}$
The coordinates of Q are $\left(-\frac{1}{2}, 0\right)$.
Now, let's determine the type of triangle QAB using the coordinates Q$\left(-\frac{1}{2}, 0\right)$, A$(-5, -2)$, and B$(4, -2)$.
We already found $QA^2 = QB^2$, which means $QA = QB$. A triangle with two sides of equal length is an isosceles triangle.
To confirm and be more specific, let's calculate the length of AB.
Calculate the squared length of the side AB:
$A = (-5, -2)$, $B = (4, -2)$
$AB^2 = (4 - (-5))^2 + (-2 - (-2))^2$
$AB^2 = (4 + 5)^2 + (-2 + 2)^2$
$AB^2 = (9)^2 + (0)^2$
$AB^2 = 81 + 0 = 81$
$AB = \sqrt{81} = 9$
Now calculate the lengths QA and QB:
$QA = \sqrt{QA^2} = \sqrt{x^2 + 10x + 29}$ where $x = -\frac{1}{2}$
$QA = \sqrt{\left(-\frac{1}{2}\right)^2 + 10\left(-\frac{1}{2}\right) + 29}$
$QA = \sqrt{\frac{1}{4} - 5 + 29}$
$QA = \sqrt{\frac{1}{4} + 24}$
$QA = \sqrt{\frac{1 + 96}{4}} = \sqrt{\frac{97}{4}} = \frac{\sqrt{97}}{2}$
Since $QA^2 = QB^2$, $QB = QA = \frac{\sqrt{97}}{2}$.
The lengths of the sides of triangle QAB are:
$QA = \frac{\sqrt{97}}{2}$
$QB = \frac{\sqrt{97}}{2}$
$AB = 9$
Since $QA = QB$, the triangle QAB is an isosceles triangle.
Note that the y-coordinates of A and B are the same (-2). This means the line segment AB is horizontal. The perpendicular bisector of a horizontal line segment is a vertical line passing through the midpoint. The x-coordinate of the midpoint of AB is $\frac{-5 + 4}{2} = -\frac{1}{2}$. So, the perpendicular bisector is the vertical line $x = -\frac{1}{2}$. The point Q lies on this line and on the x-axis (where $y=0$). Thus, the coordinates of Q are $\left(-\frac{1}{2}, 0\right)$, which matches our calculation.
The coordinates of point Q are $\left(-\frac{1}{2}, 0\right)$.
The type of triangle formed by the points Q, A, and B is an isosceles triangle.
Question 7. Find the value of m if the points (5, 1), (–2, –3) and (8, 2m ) are collinear.
Answer:
Given:
The points P (5, 1), Q (–2, –3), and R (8, 2m) are collinear.
To Find:
The value of m.
Solution:
Let the coordinates of the points be:
$P(x_1, y_1) = (5, 1)$
$Q(x_2, y_2) = (-2, -3)$
$R(x_3, y_3) = (8, 2m)$
For three points to be collinear, the area of the triangle formed by these points must be zero.
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Since the points are collinear, the area is 0:
$\frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| = 0$
This implies:
$x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) = 0$
... (1)
Substitute the coordinates of P, Q, and R into equation (1):
$5(-3 - 2m) + (-2)(2m - 1) + 8(1 - (-3)) = 0$
$5(-3 - 2m) - 2(2m - 1) + 8(1 + 3) = 0$
Expand the terms:
$-15 - 10m - 4m + 2 + 8(4) = 0$
$-15 - 10m - 4m + 2 + 32 = 0$
Combine the terms with 'm' and the constant terms:
$(-10m - 4m) + (-15 + 2 + 32) = 0$
$-14m + (-13 + 32) = 0$
$-14m + 19 = 0$
Add 14m to both sides:
$19 = 14m$
Divide by 14 to find m:
$m = \frac{19}{14}$
Alternatively, we can use the slope method. If three points P, Q, and R are collinear, the slope of PQ must be equal to the slope of QR.
Slope of PQ $= \frac{y_2 - y_1}{x_2 - x_1} = \frac{-3 - 1}{-2 - 5} = \frac{-4}{-7} = \frac{4}{7}$
Slope of QR $= \frac{y_3 - y_2}{x_3 - x_2} = \frac{2m - (-3)}{8 - (-2)} = \frac{2m + 3}{8 + 2} = \frac{2m + 3}{10}$
Equate the slopes:
$\frac{4}{7} = \frac{2m + 3}{10}$
Cross-multiply:
$4 \times 10 = 7 \times (2m + 3)$
$40 = 14m + 21$
Subtract 21 from both sides:
$40 - 21 = 14m$
$19 = 14m$
$m = \frac{19}{14}$
Both methods yield the same result.
The value of m is $\frac{19}{14}$.
Question 8. If the point A (2, – 4) is equidistant from P (3, 8) and Q (–10, y), find the values of y. Also find distance PQ.
Answer:
Given:
Point A (2, – 4).
Point P (3, 8).
Point Q (–10, y).
Point A is equidistant from P and Q, meaning AP = AQ.
To Find:
The value(s) of y.
The distance PQ.
Solution:
Since A is equidistant from P and Q, we have AP = AQ.
Squaring both sides, we get $AP^2 = AQ^2$.
Using the distance formula squared: $d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2$.
Calculate $AP^2$ using points A(2, –4) and P(3, 8):
$AP^2 = (3 - 2)^2 + (8 - (-4))^2$
$AP^2 = (1)^2 + (8 + 4)^2$
$AP^2 = 1^2 + 12^2$
$AP^2 = 1 + 144 = 145$
Calculate $AQ^2$ using points A(2, –4) and Q(–10, y):
$AQ^2 = (-10 - 2)^2 + (y - (-4))^2$
$AQ^2 = (-12)^2 + (y + 4)^2$
$AQ^2 = 144 + (y + 4)^2$
$AQ^2 = 144 + (y^2 + 8y + 16)$
$AQ^2 = y^2 + 8y + 160$
Equate $AP^2$ and $AQ^2$:
$145 = y^2 + 8y + 160$
... (1)
Rearrange the equation to form a quadratic equation in y:
$0 = y^2 + 8y + 160 - 145$
$0 = y^2 + 8y + 15$
Factor the quadratic equation. We look for two numbers that multiply to 15 and add up to 8. These numbers are 3 and 5.
$y^2 + 3y + 5y + 15 = 0$
$y(y + 3) + 5(y + 3) = 0$
$(y + 3)(y + 5) = 0$
This gives two possible values for y:
Case 1: $y + 3 = 0 \implies y = -3$
Case 2: $y + 5 = 0 \implies y = -5$
The possible values for y are -3 and -5.
Now, we need to find the distance PQ for each possible value of y.
Points P are (3, 8) and Q are (–10, y).
Case 1: y = -3
Q is (–10, –3).
$PQ = \sqrt{(-10 - 3)^2 + (-3 - 8)^2}$
$PQ = \sqrt{(-13)^2 + (-11)^2}$
$PQ = \sqrt{169 + 121}$
$PQ = \sqrt{290}$
Case 2: y = -5
Q is (–10, –5).
$PQ = \sqrt{(-10 - 3)^2 + (-5 - 8)^2}$
$PQ = \sqrt{(-13)^2 + (-13)^2}$
$PQ = \sqrt{169 + 169}$
$PQ = \sqrt{2 \times 169}$
$PQ = 13\sqrt{2}$
The values of y are -3 and -5.
The distance PQ is $\sqrt{290}$ units when y = -3, and $13\sqrt{2}$ units when y = -5.
Question 9. Find the area of the triangle whose vertices are (–8, 4), (–6, 6) and (–3, 9).
Answer:
Given:
The vertices of the triangle are A (–8, 4), B (–6, 6), and C (–3, 9).
To Find:
The area of the triangle ABC.
Solution:
Let the coordinates of the vertices be:
$(x_1, y_1) = (-8, 4)$
$(x_2, y_2) = (-6, 6)$
$(x_3, y_3) = (-3, 9)$
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by the formula:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Substitute the given coordinates into the formula:
Area $= \frac{1}{2} |(-8)(6 - 9) + (-6)(9 - 4) + (-3)(4 - 6)|$
Area $= \frac{1}{2} |(-8)(-3) + (-6)(5) + (-3)(-2)|$
Area $= \frac{1}{2} |24 - 30 + 6|$
Area $= \frac{1}{2} |-6 + 6|$
Area $= \frac{1}{2} |0|$
Area $= 0$
Since the area of the triangle formed by the given points is 0, the points A, B, and C are collinear.
When three points are collinear, they do not form a triangle in the standard sense, and the area is zero.
The area of the triangle is 0 square units.
Question 10. In what ratio does the x–axis divide the line segment joining the points (– 4, – 6) and (–1, 7)? Find the coordinates of the point of division.
Answer:
Given:
The line segment joining the points A (– 4, – 6) and B (–1, 7).
The x-axis divides this line segment.
To Find:
The ratio in which the x-axis divides the line segment AB.
The coordinates of the point of division.
Solution:
Let the point where the x-axis divides the line segment AB be P $(x, y)$.
Since the point P lies on the x-axis, its y-coordinate is 0. So, the coordinates of P are $(x, 0)$.
Let the x-axis divide the line segment AB in the ratio $m : n$.
Using the section formula, the coordinates of the point P $(x, y)$ dividing the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ in the ratio $m : n$ internally are:
$x = \frac{nx_1 + mx_2}{m + n}$
$y = \frac{ny_1 + my_2}{m + n}$
Here, $(x_1, y_1) = (-4, -6)$, $(x_2, y_2) = (-1, 7)$, and $(x, y) = (x, 0)$.
Substitute the values into the y-coordinate formula, since we know the y-coordinate of P is 0:
$0 = \frac{n(-6) + m(7)}{m + n}$
... (1)
Multiply both sides by $(m + n)$:
$0 \times (m + n) = -6n + 7m$
$0 = -6n + 7m$
Rearrange the equation:
$6n = 7m$
To find the ratio $m : n$, divide both sides by $7n$:
$\frac{6n}{7n} = \frac{7m}{7n}$
$\frac{6}{7} = \frac{m}{n}$
So, the ratio $m : n$ is 6 : 7.
Now, we find the x-coordinate of the point of division P using the section formula and the ratio $m : n = 6 : 7$.
$x = \frac{nx_1 + mx_2}{m + n}$
$x = \frac{7(-4) + 6(-1)}{6 + 7}$
$x = \frac{-28 - 6}{13}$
$x = \frac{-34}{13}$
The coordinates of the point of division P are $\left(-\frac{34}{13}, 0\right)$.
The x-axis divides the line segment in the ratio 6 : 7.
The coordinates of the point of division are $\left(-\frac{34}{13}, 0\right)$.
Question 11. Find the ratio in which the point P $\left( \frac{3}{4} , \frac{5}{12} \right)$ divides the line segment joining the points A $\left( \frac{1}{2} , \frac{3}{2} \right)$ and B (2, –5).
Answer:
Given:
Point A $\left( \frac{1}{2}, \frac{3}{2} \right)$.
Point B $(2, -5)$.
Point P $\left( \frac{3}{4}, \frac{5}{12} \right)$ divides the line segment AB.
To Find:
The ratio in which point P divides the line segment AB.
Solution:
Let the coordinates of point A be $(x_1, y_1) = \left(\frac{1}{2}, \frac{3}{2}\right)$.
Let the coordinates of point B be $(x_2, y_2) = (2, -5)$.
Let the coordinates of the dividing point P be $(x, y) = \left(\frac{3}{4}, \frac{5}{12}\right)$.
Let the point P divide the line segment AB in the ratio $k : 1$.
Using the section formula, the coordinates of the point P $(x, y)$ dividing the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ in the ratio $k : 1$ are:
$x = \frac{kx_2 + 1 \cdot x_1}{k + 1} = \frac{kx_2 + x_1}{k+1}$
$y = \frac{ky_2 + 1 \cdot y_1}{k + 1} = \frac{ky_2 + y_1}{k+1}$
Substitute the given coordinates into the formula for the x-coordinate:
$\frac{3}{4} = \frac{k(2) + \frac{1}{2}}{k + 1}$
... (1)
Simplify the equation:
$\frac{3}{4} = \frac{2k + \frac{1}{2}}{k + 1}$
$\frac{3}{4} = \frac{\frac{4k + 1}{2}}{k + 1}$
$\frac{3}{4} = \frac{4k + 1}{2(k + 1)}$
Cross-multiply:
$3 \cdot 2(k + 1) = 4(4k + 1)$
$6(k + 1) = 4(4k + 1)$
$6k + 6 = 16k + 4$
Rearrange the terms to solve for k:
$6 - 4 = 16k - 6k$
$2 = 10k$
$k = \frac{2}{10} = \frac{1}{5}$
The ratio $k : 1$ is $\frac{1}{5} : 1$.
To express this ratio in the form $m : n$ where m and n are integers, multiply both parts of the ratio by 5:
$\left(\frac{1}{5} \times 5\right) : (1 \times 5) = 1 : 5$
We can verify this ratio using the y-coordinate formula:
$\frac{5}{12} = \frac{k(-5) + \frac{3}{2}}{k + 1}$
... (2)
Substitute $k = \frac{1}{5}$ into equation (2):
$\frac{5}{12} = \frac{\frac{1}{5}(-5) + \frac{3}{2}}{\frac{1}{5} + 1}$
$\frac{5}{12} = \frac{-1 + \frac{3}{2}}{\frac{1 + 5}{5}}$
$\frac{5}{12} = \frac{\frac{-2 + 3}{2}}{\frac{6}{5}}$
$\frac{5}{12} = \frac{\frac{1}{2}}{\frac{6}{5}}$
$\frac{5}{12} = \frac{1}{2} \times \frac{5}{6}$
$\frac{5}{12} = \frac{5}{12}$
The ratio $1 : 5$ is confirmed by the y-coordinates.
The ratio in which the point P divides the line segment joining A and B is 1 : 5.
Question 12. If P (9a – 2, –b) divides line segment joining A (3a + 1, –3) and B (8a, 5) in the ratio 3 : 1, find the values of a and b.
Answer:
Given:
Point A $(3a + 1, -3)$.
Point B $(8a, 5)$.
Point P $(9a - 2, -b)$ divides the line segment AB in the ratio 3 : 1.
To Find:
The values of a and b.
Solution:
Let the coordinates of point A be $(x_1, y_1) = (3a + 1, -3)$.
Let the coordinates of point B be $(x_2, y_2) = (8a, 5)$.
Let the coordinates of the dividing point P be $(x, y) = (9a - 2, -b)$.
The ratio of division is $m : n = 3 : 1$.
Using the section formula, the coordinates of the point P $(x, y)$ dividing the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ in the ratio $m : n$ internally are:
$x = \frac{mx_2 + nx_1}{m + n}$
$y = \frac{my_2 + ny_1}{m + n}$
Substitute the given values into the x-coordinate formula:
$9a - 2 = \frac{3(8a) + 1(3a + 1)}{3 + 1}$
$9a - 2 = \frac{24a + 3a + 1}{4}$
$9a - 2 = \frac{27a + 1}{4}$
Multiply both sides by 4:
$4(9a - 2) = 27a + 1$
$36a - 8 = 27a + 1$
Rearrange the terms to solve for a:
$36a - 27a = 1 + 8$
$9a = 9$
$a = \frac{9}{9} = 1$
Now substitute the given values into the y-coordinate formula:
$-b = \frac{3(5) + 1(-3)}{3 + 1}$
$-b = \frac{15 - 3}{4}$
$-b = \frac{12}{4}$
$-b = 3$
Multiply both sides by -1:
$b = -3$
The value of a is 1 and the value of b is -3.
Question 13. If (a, b) is the mid-point of the line segment joining the points A (10, –6) and B (k, 4) and a – 2b = 18, find the value of k and the distance AB.
Answer:
Given:
Point A (10, –6).
Point B (k, 4).
Point (a, b) is the mid-point of the line segment AB.
The coordinates (a, b) satisfy the equation $a - 2b = 18$.
To Find:
The value of k.
The distance AB.
Solution:
Let the coordinates of point A be $(x_1, y_1) = (10, -6)$.
Let the coordinates of point B be $(x_2, y_2) = (k, 4)$.
Let the coordinates of the mid-point be $(a, b)$.
Using the mid-point formula, the coordinates of the mid-point of a line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ are $\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)$.
So, the coordinates of the mid-point (a, b) are:
$a = \frac{10 + k}{2}$
$b = \frac{-6 + 4}{2} = \frac{-2}{2} = -1$
We are given that the coordinates (a, b) satisfy the equation $a - 2b = 18$.
We have found $b = -1$. Substitute this value into the equation:
$a - 2(-1) = 18$
... (1)
$a + 2 = 18$
Subtract 2 from both sides:
$a = 18 - 2$
$a = 16$
Now we use the value of a to find k. We know $a = \frac{10 + k}{2}$.
Substitute $a = 16$ into this equation:
$16 = \frac{10 + k}{2}$
... (2)
Multiply both sides by 2:
$16 \times 2 = 10 + k$
$32 = 10 + k$
Subtract 10 from both sides:
$k = 32 - 10$
$k = 22$
So, the coordinates of point B are (22, 4).
Now we need to find the distance AB using points A(10, –6) and B(22, 4).
Using the distance formula, the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
$AB = \sqrt{(22 - 10)^2 + (4 - (-6))^2}$
$AB = \sqrt{(12)^2 + (4 + 6)^2}$
$AB = \sqrt{12^2 + 10^2}$
$AB = \sqrt{144 + 100}$
$AB = \sqrt{244}$
We can simplify the square root $\sqrt{244}$. $244 = 4 \times 61$.
$AB = \sqrt{4 \times 61} = \sqrt{4} \times \sqrt{61} = 2\sqrt{61}$
The value of k is 22.
The distance AB is $2\sqrt{61}$ units.
Question 14. The centre of a circle is (2a, a – 7). Find the values of a if the circle passes through the point (11, –9) and has diameter 10$\sqrt{2}$ units.
Answer:
Given:
The centre of the circle is C (2a, a – 7).
The circle passes through the point P (11, –9).
The diameter of the circle is $10\sqrt{2}$ units.
To Find:
The value(s) of a.
Solution:
The radius of the circle is half of the diameter.
Radius $(r) = \frac{\text{Diameter}}{2} = \frac{10\sqrt{2}}{2} = 5\sqrt{2}$ units.
The distance from the centre of the circle to any point on the circle is equal to the radius.
The distance between the centre C (2a, a – 7) and the point P (11, –9) is equal to the radius ($5\sqrt{2}$).
$CP = r$
$CP = 5\sqrt{2}$
Using the distance formula, the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Let $(x_1, y_1) = (2a, a – 7)$ and $(x_2, y_2) = (11, –9)$.
$CP = \sqrt{(11 - 2a)^2 + (-9 - (a - 7))^2}$
$CP = \sqrt{(11 - 2a)^2 + (-9 - a + 7)^2}$
$CP = \sqrt{(11 - 2a)^2 + (-a - 2)^2}$
$CP = \sqrt{(11 - 2a)^2 + (a + 2)^2}$
We know $CP = 5\sqrt{2}$. So, we can set up the equation:
$\sqrt{(11 - 2a)^2 + (a + 2)^2} = 5\sqrt{2}$
... (1)
Squaring both sides of the equation:
$(11 - 2a)^2 + (a + 2)^2 = (5\sqrt{2})^2$
$(11 - 2a)^2 + (a + 2)^2 = 25 \times 2$
$(11 - 2a)^2 + (a + 2)^2 = 50$
Expand the squared terms:
$(11^2 - 2 \cdot 11 \cdot 2a + (2a)^2) + (a^2 + 2 \cdot a \cdot 2 + 2^2) = 50$
$(121 - 44a + 4a^2) + (a^2 + 4a + 4) = 50$
Combine like terms:
$(4a^2 + a^2) + (-44a + 4a) + (121 + 4 - 50) = 0$
$5a^2 - 40a + 75 = 0$
This is a quadratic equation in 'a'. We can simplify it by dividing the entire equation by 5:
$a^2 - 8a + 15 = 0$
... (2)
Factor the quadratic equation. We look for two numbers that multiply to 15 and add up to -8. These numbers are -3 and -5.
$a^2 - 3a - 5a + 15 = 0$
$a(a - 3) - 5(a - 3) = 0$
$(a - 3)(a - 5) = 0$
This gives two possible values for a:
Case 1: $a - 3 = 0 \implies a = 3$
Case 2: $a - 5 = 0 \implies a = 5$
The values of a are 3 and 5.
Question 15. The line segment joining the points A (3, 2) and B (5,1) is divided at the point P in the ratio 1:2 and it lies on the line 3x – 18y + k = 0. Find the value of k.
Answer:
Given:
Point A (3, 2).
Point B (5, 1).
Point P divides the line segment AB in the ratio 1 : 2.
Point P lies on the line $3x - 18y + k = 0$.
To Find:
The value of k.
Solution:
Let the coordinates of point A be $(x_1, y_1) = (3, 2)$.
Let the coordinates of point B be $(x_2, y_2) = (5, 1)$.
Let the coordinates of the dividing point P be $(x, y)$.
The ratio of division is $m : n = 1 : 2$.
Using the section formula, the coordinates of the point P $(x, y)$ dividing the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ in the ratio $m : n$ internally are:
$x = \frac{mx_2 + nx_1}{m + n}$
$y = \frac{my_2 + ny_1}{m + n}$
Substitute the given values to find the coordinates of P:
$x = \frac{1(5) + 2(3)}{1 + 2} = \frac{5 + 6}{3} = \frac{11}{3}$
$y = \frac{1(1) + 2(2)}{1 + 2} = \frac{1 + 4}{3} = \frac{5}{3}$
So, the coordinates of point P are $\left(\frac{11}{3}, \frac{5}{3}\right)$.
We are given that the point P $\left(\frac{11}{3}, \frac{5}{3}\right)$ lies on the line $3x - 18y + k = 0$.
This means the coordinates of P must satisfy the equation of the line.
Substitute $x = \frac{11}{3}$ and $y = \frac{5}{3}$ into the equation of the line:
$3\left(\frac{11}{3}\right) - 18\left(\frac{5}{3}\right) + k = 0$
... (1)
Simplify the equation:
$\cancel{3} \times \frac{11}{\cancel{3}} - \cancel{18}^6 \times \frac{5}{\cancel{3}} + k = 0$
$11 - 6 \times 5 + k = 0$
$11 - 30 + k = 0$
$-19 + k = 0$
Add 19 to both sides:
$k = 19$
The value of k is 19.
Question 16. If D $\left( \frac{-1}{2} , \frac{5}{2} \right)$ , E (7, 3) and F $\left( \frac{7}{2} , \frac{7}{2} \right)$ are the midpoints of sides of Δ ABC, find the area of the Δ ABC.
Answer:
Given:
The midpoints of the sides of Δ ABC are D $\left(-\frac{1}{2}, \frac{5}{2}\right)$, E (7, 3), and F $\left(\frac{7}{2}, \frac{7}{2}\right)$.
To Find:
The area of Δ ABC.
Solution:
We can find the area of Δ ABC using the property that the area of the triangle formed by joining the midpoints of the sides of a given triangle is one-fourth the area of the original triangle.
Area(ABC) $= 4 \times$ Area(DEF)
We first calculate the area of Δ DEF using the coordinates of the midpoints.
Let the coordinates of the vertices of Δ DEF be:
$D(x_1, y_1) = \left(-\frac{1}{2}, \frac{5}{2}\right)$
$E(x_2, y_2) = (7, 3)$
$F(x_3, y_3) = \left(\frac{7}{2}, \frac{7}{2}\right)$
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by the formula:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Substitute the coordinates of D, E, and F into the formula:
Area(DEF) $= \frac{1}{2} \left| -\frac{1}{2}\left(3 - \frac{7}{2}\right) + 7\left(\frac{7}{2} - \frac{5}{2}\right) + \frac{7}{2}\left(\frac{5}{2} - 3\right) \right|$
Calculate the terms inside the absolute value:
$3 - \frac{7}{2} = \frac{6}{2} - \frac{7}{2} = -\frac{1}{2}$
$\frac{7}{2} - \frac{5}{2} = \frac{2}{2} = 1$
$\frac{5}{2} - 3 = \frac{5}{2} - \frac{6}{2} = -\frac{1}{2}$
Substitute these values back into the area formula:
Area(DEF) $= \frac{1}{2} \left| -\frac{1}{2}\left(-\frac{1}{2}\right) + 7(1) + \frac{7}{2}\left(-\frac{1}{2}\right) \right|$
Area(DEF) $= \frac{1}{2} \left| \frac{1}{4} + 7 - \frac{7}{4} \right|$
Area(DEF) $= \frac{1}{2} \left| \frac{1}{4} + \frac{28}{4} - \frac{7}{4} \right|$
Area(DEF) $= \frac{1}{2} \left| \frac{1 + 28 - 7}{4} \right|$
Area(DEF) $= \frac{1}{2} \left| \frac{22}{4} \right|$
Area(DEF) $= \frac{1}{2} \left| \frac{11}{2} \right|$
Area(DEF) $= \frac{1}{2} \times \frac{11}{2} = \frac{11}{4}$ square units.
Now, find the area of Δ ABC:
Area(ABC) $= 4 \times$ Area(DEF)
Area(ABC) $= 4 \times \frac{11}{4}$
Area(ABC) $= 11$ square units.
The area of Δ ABC is 11 square units.
Question 17. The points A (2, 9), B (a, 5) and C (5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ΔABC.
Answer:
Given:
The vertices of Δ ABC are A (2, 9), B (a, 5), and C (5, 5).
Δ ABC is right-angled at B.
To Find:
The value(s) of a.
The area of Δ ABC.
Solution:
Since the triangle is right-angled at B, the sides AB and BC are perpendicular to each other. The product of the slopes of two perpendicular lines is -1 (provided neither line is vertical or horizontal).
Calculate the slope of AB:
Slope of AB $(m_{AB}) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{5 - 9}{a - 2} = \frac{-4}{a - 2}$
Calculate the slope of BC:
Slope of BC $(m_{BC}) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{5 - 5}{5 - a} = \frac{0}{5 - a}$
Since AB $\perp$ BC, the product of their slopes is -1, unless one is vertical and the other is horizontal.
The slope of BC is 0, which means BC is a horizontal line. For AB to be perpendicular to a horizontal line, AB must be a vertical line. A vertical line has an undefined slope, meaning the denominator of the slope is 0.
For the slope of AB, $m_{AB} = \frac{-4}{a - 2}$, to be undefined, the denominator must be zero:
$a - 2 = 0$
$a = 2$
If $a=2$, point B is (2, 5) and point A is (2, 9). AB is a vertical line ($x=2$).
Point B is (2, 5) and point C is (5, 5). BC is a horizontal line ($y=5$).
A vertical line and a horizontal line are perpendicular. Thus, the triangle is right-angled at B when $a=2$.
The value of a is 2.
Now, we find the area of ΔABC with vertices A (2, 9), B (2, 5), and C (5, 5).
Since it is a right-angled triangle at B, we can use the lengths of the perpendicular sides AB and BC as the base and height.
Calculate the length of side AB using the distance formula or simply by finding the difference in y-coordinates since it's a vertical line:
$A = (2, 9)$, $B = (2, 5)$
$AB = \sqrt{(2 - 2)^2 + (5 - 9)^2} = \sqrt{0^2 + (-4)^2} = \sqrt{0 + 16} = \sqrt{16} = 4$ units.
Calculate the length of side BC using the distance formula or simply by finding the difference in x-coordinates since it's a horizontal line:
$B = (2, 5)$, $C = (5, 5)$
$BC = \sqrt{(5 - 2)^2 + (5 - 5)^2} = \sqrt{3^2 + 0^2} = \sqrt{9 + 0} = \sqrt{9} = 3$ units.
The area of a right-angled triangle is given by $\frac{1}{2} \times \text{base} \times \text{height}$.
Using AB and BC as the base and height:
Area(ABC) $= \frac{1}{2} \times AB \times BC$
Area(ABC) $= \frac{1}{2} \times 4 \times 3$
Area(ABC) $= \frac{1}{2} \times 12$
Area(ABC) $= 6$ square units.
Alternatively, use the area formula for a triangle with vertices A (2, 9), B (2, 5), and C (5, 5):
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Area $= \frac{1}{2} |2(5 - 5) + 2(5 - 9) + 5(9 - 5)|$
Area $= \frac{1}{2} |2(0) + 2(-4) + 5(4)|$
Area $= \frac{1}{2} |0 - 8 + 20|$
Area $= \frac{1}{2} |12|$
Area $= \frac{1}{2} \times 12 = 6$ square units.
The value of a is 2.
The area of ΔABC is 6 square units.
Question 18. Find the coordinates of the point R on the line segment joining the points P (–1, 3) and Q (2, 5) such that PR = $\frac{3}{5}$ PQ
Answer:
Given:
Point P (–1, 3).
Point Q (2, 5).
Point R lies on the line segment PQ such that PR = $\frac{3}{5}$ PQ.
To Find:
The coordinates of point R.
Solution:
The condition PR = $\frac{3}{5}$ PQ tells us about the relative lengths of the segments PR and RQ.
Since R lies on the line segment PQ, we have PQ = PR + RQ.
Substitute the given condition into this equation:
PQ = $\frac{3}{5}$ PQ + RQ
Subtract $\frac{3}{5}$ PQ from both sides:
PQ - $\frac{3}{5}$ PQ = RQ
$\left(1 - \frac{3}{5}\right)$ PQ = RQ
$\frac{5 - 3}{5}$ PQ = RQ
$\frac{2}{5}$ PQ = RQ
Now consider the ratio of the lengths PR and RQ:
$\frac{PR}{RQ} = \frac{\frac{3}{5} PQ}{\frac{2}{5} PQ} = \frac{3/5}{2/5} = \frac{3}{2}$
So, point R divides the line segment PQ in the ratio $PR : RQ = 3 : 2$.
Let the coordinates of point P be $(x_1, y_1) = (-1, 3)$.
Let the coordinates of point Q be $(x_2, y_2) = (2, 5)$.
Let the coordinates of point R be $(x, y)$.
The ratio of division is $m : n = 3 : 2$.
Using the section formula, the coordinates of the point R $(x, y)$ dividing the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ in the ratio $m : n$ internally are:
$x = \frac{mx_2 + nx_1}{m + n}$
$y = \frac{my_2 + ny_1}{m + n}$
Substitute the given values into the formula for the x-coordinate:
$x = \frac{3(2) + 2(-1)}{3 + 2} = \frac{6 - 2}{5} = \frac{4}{5}$
Substitute the given values into the formula for the y-coordinate:
$y = \frac{3(5) + 2(3)}{3 + 2} = \frac{15 + 6}{5} = \frac{21}{5}$
The coordinates of point R are $\left(\frac{4}{5}, \frac{21}{5}\right)$.
Question 19. Find the values of k if the points A (k + 1, 2k), B (3k, 2k + 3) and C (5k – 1, 5k) are collinear.
Answer:
Given:
The points A (k + 1, 2k), B (3k, 2k + 3), and C (5k – 1, 5k) are collinear.
To Find:
The value(s) of k.
Solution:
For three points to be collinear, the slope of the line segment joining any two pairs of points must be equal.
Let the points be A $(x_1, y_1)$, B $(x_2, y_2)$, and C $(x_3, y_3)$.
$(x_1, y_1) = (k + 1, 2k)$
$(x_2, y_2) = (3k, 2k + 3)$
$(x_3, y_3) = (5k - 1, 5k)$
Calculate the slope of AB ($m_{AB}$):
$m_{AB} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{(2k + 3) - (2k)}{(3k) - (k + 1)} = \frac{2k + 3 - 2k}{3k - k - 1} = \frac{3}{2k - 1}$
Calculate the slope of BC ($m_{BC}$):
$m_{BC} = \frac{y_3 - y_2}{x_3 - x_2} = \frac{(5k) - (2k + 3)}{(5k - 1) - (3k)} = \frac{5k - 2k - 3}{5k - 1 - 3k} = \frac{3k - 3}{2k - 1}$
For points A, B, and C to be collinear, $m_{AB} = m_{BC}$.
$\frac{3}{2k - 1} = \frac{3k - 3}{2k - 1}$
... (1)
We must consider two cases: when the denominator $2k - 1 = 0$ and when $2k - 1 \neq 0$.
Case 1: $2k - 1 = 0$
This implies $k = \frac{1}{2}$.
If $k = \frac{1}{2}$, the coordinates are:
A $\left(\frac{1}{2} + 1, 2\left(\frac{1}{2}\right)\right) = \left(\frac{3}{2}, 1\right)$
B $\left(3\left(\frac{1}{2}\right), 2\left(\frac{1}{2}\right) + 3\right) = \left(\frac{3}{2}, 1 + 3\right) = \left(\frac{3}{2}, 4\right)$
C $\left(5\left(\frac{1}{2}\right) - 1, 5\left(\frac{1}{2}\right)\right) = \left(\frac{5}{2} - 1, \frac{5}{2}\right) = \left(\frac{3}{2}, \frac{5}{2}\right)$
Since the x-coordinates of A, B, and C are all $\frac{3}{2}$, these points lie on the vertical line $x = \frac{3}{2}$. Points on a vertical line are collinear. Therefore, the points are collinear when $k = \frac{1}{2}$.
Case 2: $2k - 1 \neq 0$
From equation (1), we can multiply both sides by $(2k - 1)$:
$3 = 3k - 3$
Add 3 to both sides:
$3 + 3 = 3k$
$6 = 3k$
Divide by 3:
$k = \frac{6}{3} = 2$
If $k = 2$, the slopes $m_{AB} = \frac{3}{2(2)-1} = \frac{3}{3} = 1$ and $m_{BC} = \frac{3(2)-3}{2(2)-1} = \frac{6-3}{3} = \frac{3}{3} = 1$. Since $m_{AB} = m_{BC}$, the points are collinear.
The values of k for which the points are collinear are $\frac{1}{2}$ and 2.
Alternate Solution (Using Area of Triangle):
The area of the triangle formed by three collinear points is zero.
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| = 0$
Substituting the coordinates and setting the expression inside the absolute value to zero gives the equation:
$(k + 1)((2k + 3) - 5k) + (3k)(5k - 2k) + (5k - 1)(2k - (2k + 3)) = 0$
$(k + 1)(-3k + 3) + (3k)(3k) + (5k - 1)(-3) = 0$
Expanding and simplifying this equation:
$(-3k^2 + 3k - 3k + 3) + 9k^2 + (-15k + 3) = 0$
$-3k^2 + 3 + 9k^2 - 15k + 3 = 0$
Combine like terms:
$6k^2 - 15k + 6 = 0$
... (Quadratic Equation)
Divide by 3:
$2k^2 - 5k + 2 = 0$
Factor the quadratic equation:
$2k^2 - k - 4k + 2 = 0$
$k(2k - 1) - 2(2k - 1) = 0$
$(2k - 1)(k - 2) = 0$
Setting each factor to zero gives the values of k:
$2k - 1 = 0 \implies k = \frac{1}{2}$
$k - 2 = 0 \implies k = 2$
This confirms the values obtained using the slope method.
The values of k are $\frac{1}{2}$ and 2.
Question 20. Find the ratio in which the line 2x + 3y – 5 = 0 divides the line segment joining the points (8, –9) and (2, 1). Also find the coordinates of the point of division.
Answer:
Given:
Point A (8, –9).
Point B (2, 1).
The line $2x + 3y – 5 = 0$ divides the line segment AB.
To Find:
The ratio in which the line divides the line segment AB.
The coordinates of the point of division.
Solution:
Let the point where the line $2x + 3y – 5 = 0$ divides the line segment joining A (8, –9) and B (2, 1) be P $(x, y)$.
Let the ratio in which the line divides the line segment AB be $k : 1$.
Using the section formula, the coordinates of the point P $(x, y)$ dividing the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ in the ratio $k : 1$ internally are:
$x = \frac{kx_2 + 1 \cdot x_1}{k + 1} = \frac{kx_2 + x_1}{k+1}$
$y = \frac{ky_2 + 1 \cdot y_1}{k + 1} = \frac{ky_2 + y_1}{k+1}$
Here, $(x_1, y_1) = (8, -9)$ and $(x_2, y_2) = (2, 1)$.
$x = \frac{k(2) + 1(8)}{k + 1} = \frac{2k + 8}{k + 1}$
$y = \frac{k(1) + 1(-9)}{k + 1} = \frac{k - 9}{k + 1}$
So, the coordinates of the point of division P are $\left(\frac{2k + 8}{k + 1}, \frac{k - 9}{k + 1}\right)$.
Since the point P lies on the line $2x + 3y – 5 = 0$, its coordinates must satisfy the equation of the line.
Substitute the x and y coordinates of P into the equation of the line:
$2\left(\frac{2k + 8}{k + 1}\right) + 3\left(\frac{k - 9}{k + 1}\right) - 5 = 0$
... (1)
Multiply the entire equation by $(k + 1)$ to clear the denominators (assuming $k \neq -1$):
$2(2k + 8) + 3(k - 9) - 5(k + 1) = 0$
Expand and simplify the equation:
$4k + 16 + 3k - 27 - 5k - 5 = 0$
Combine the terms with 'k' and the constant terms:
$(4k + 3k - 5k) + (16 - 27 - 5) = 0$
$2k + (-11 - 5) = 0$
$2k - 16 = 0$
Add 16 to both sides:
$2k = 16$
Divide by 2:
$k = \frac{16}{2} = 8$
The ratio $k : 1$ is $8 : 1$.
Since k is positive, the division is internal.
Now, we find the coordinates of the point of division P using $k = 8$ and the section formula:
$x = \frac{2k + 8}{k + 1} = \frac{2(8) + 8}{8 + 1} = \frac{16 + 8}{9} = \frac{24}{9} = \frac{8}{3}$
$y = \frac{k - 9}{k + 1} = \frac{8 - 9}{8 + 1} = \frac{-1}{9}$
The coordinates of the point of division P are $\left(\frac{8}{3}, -\frac{1}{9}\right)$.
Alternate Method for Ratio:
Let the ratio be $m : n$. The point of division P $(x, y)$ lies on the line $2x + 3y - 5 = 0$.
Using the section formula:
$x = \frac{mx_2 + nx_1}{m + n} = \frac{m(2) + n(8)}{m + n} = \frac{2m + 8n}{m + n}$
$y = \frac{my_2 + ny_1}{m + n} = \frac{m(1) + n(-9)}{m + n} = \frac{m - 9n}{m + n}$
Substitute these into the equation of the line $2x + 3y - 5 = 0$:
$2\left(\frac{2m + 8n}{m + n}\right) + 3\left(\frac{m - 9n}{m + n}\right) - 5 = 0$
Multiply by $(m + n)$: (assuming $m+n \neq 0$)
$2(2m + 8n) + 3(m - 9n) - 5(m + n) = 0$
$4m + 16n + 3m - 27n - 5m - 5n = 0$
Combine like terms:
$(4m + 3m - 5m) + (16n - 27n - 5n) = 0$
$2m + (-11n - 5n) = 0$
$2m - 16n = 0$
$2m = 16n$
Divide by $2n$ (assuming $n \neq 0$):
$\frac{2m}{2n} = \frac{16n}{2n}$
$\frac{m}{n} = \frac{16}{2} = 8$
So, the ratio $m : n$ is 8 : 1.
The ratio in which the line divides the line segment is 8 : 1 (internally).
The coordinates of the point of division are $\left(\frac{8}{3}, -\frac{1}{9}\right)$.
Sample Question 1 (Before Exercise 7.4)
Sample Question 1: The mid-points D, E, F of the sides of a triangle ABC are (3, 4), (8, 9) and (6, 7). Find the coordinates of the vertices of the triangle.
Answer:
Given:
The mid-points of the sides of a triangle ABC are D (3, 4), E (8, 9), and F (6, 7).
To Find:
The coordinates of the vertices A, B, and C of the triangle.
Solution:
Let the coordinates of the vertices of Δ ABC be A $(x_1, y_1)$, B $(x_2, y_2)$, and C $(x_3, y_3)$.
Let D (3, 4) be the mid-point of side AB.
Let E (8, 9) be the mid-point of side BC.
Let F (6, 7) be the mid-point of side CA.
Using the mid-point formula, the coordinates of the mid-point of a line segment joining $(x_a, y_a)$ and $(x_b, y_b)$ are $\left(\frac{x_a+x_b}{2}, \frac{y_a+y_b}{2}\right)$.
Applying the mid-point formula for each side:
1. D (3, 4) is the mid-point of AB:
$\frac{x_1 + x_2}{2} = 3 \implies x_1 + x_2 = 6$
... (1)
$\frac{y_1 + y_2}{2} = 4 \implies y_1 + y_2 = 8$
... (2)
2. E (8, 9) is the mid-point of BC:
$\frac{x_2 + x_3}{2} = 8 \implies x_2 + x_3 = 16$
... (3)
$\frac{y_2 + y_3}{2} = 9 \implies y_2 + y_3 = 18$
... (4)
3. F (6, 7) is the mid-point of CA:
$\frac{x_3 + x_1}{2} = 6 \implies x_3 + x_1 = 12$
... (5)
$\frac{y_3 + y_1}{2} = 7 \implies y_3 + y_1 = 14$
... (6)
We have a system of linear equations for the x-coordinates:
$x_1 + x_2 = 6$ (1)
$x_2 + x_3 = 16$ (3)
$x_3 + x_1 = 12$ (5)
Adding equations (1), (3), and (5):
$(x_1 + x_2) + (x_2 + x_3) + (x_3 + x_1) = 6 + 16 + 12$
$2x_1 + 2x_2 + 2x_3 = 34$
$2(x_1 + x_2 + x_3) = 34$
$x_1 + x_2 + x_3 = 17$
... (7)
Subtract equation (1) from equation (7):
$(x_1 + x_2 + x_3) - (x_1 + x_2) = 17 - 6$
$x_3 = 11$
Subtract equation (3) from equation (7):
$(x_1 + x_2 + x_3) - (x_2 + x_3) = 17 - 16$
$x_1 = 1$
Subtract equation (5) from equation (7):
$(x_1 + x_2 + x_3) - (x_3 + x_1) = 17 - 12$
$x_2 = 5$
The x-coordinates are $x_1 = 1$, $x_2 = 5$, $x_3 = 11$.
We have a system of linear equations for the y-coordinates:
$y_1 + y_2 = 8$ (2)
$y_2 + y_3 = 18$ (4)
$y_3 + y_1 = 14$ (6)
Adding equations (2), (4), and (6):
$(y_1 + y_2) + (y_2 + y_3) + (y_3 + y_1) = 8 + 18 + 14$
$2y_1 + 2y_2 + 2y_3 = 40$
$2(y_1 + y_2 + y_3) = 40$
$y_1 + y_2 + y_3 = 20$
... (8)
Subtract equation (2) from equation (8):
$(y_1 + y_2 + y_3) - (y_1 + y_2) = 20 - 8$
$y_3 = 12$
Subtract equation (4) from equation (8):
$(y_1 + y_2 + y_3) - (y_2 + y_3) = 20 - 18$
$y_1 = 2$
Subtract equation (6) from equation (8):
$(y_1 + y_2 + y_3) - (y_3 + y_1) = 20 - 14$
$y_2 = 6$
The y-coordinates are $y_1 = 2$, $y_2 = 6$, $y_3 = 12$.
The coordinates of the vertices of triangle ABC are:
A $(x_1, y_1) = \textbf{(1, 2)}$
B $(x_2, y_2) = \textbf{(5, 6)}$
C $(x_3, y_3) = \textbf{(11, 12)}$
Exercise 7.4
Question 1. If (– 4, 3) and (4, 3) are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
Answer:
Given:
Two vertices of an equilateral triangle are A (– 4, 3) and B (4, 3).
The origin (0, 0) lies in the interior of the triangle.
To Find:
The coordinates of the third vertex C $(x, y)$.
Solution:
Let the third vertex be C $(x, y)$.
In an equilateral triangle, all sides are equal in length.
$AB = BC = CA$
$AB^2 = BC^2 = CA^2$
First, calculate the squared length of the side AB:
$A = (-4, 3)$, $B = (4, 3)$
$AB^2 = (4 - (-4))^2 + (3 - 3)^2$
$AB^2 = (4 + 4)^2 + (0)^2$
$AB^2 = 8^2 + 0 = 64$
$AB = \sqrt{64} = 8$
Now, set $BC^2 = AB^2$ using points B $(4, 3)$ and C $(x, y)$:
$BC^2 = (x - 4)^2 + (y - 3)^2$
$BC^2 = x^2 - 8x + 16 + y^2 - 6y + 9$
$BC^2 = x^2 + y^2 - 8x - 6y + 25$
Equate $BC^2$ to $AB^2 = 64$:
$x^2 + y^2 - 8x - 6y + 25 = 64$
... (1)
Next, set $CA^2 = AB^2$ using points C $(x, y)$ and A $(-4, 3)$:
$CA^2 = (x - (-4))^2 + (y - 3)^2$
$CA^2 = (x + 4)^2 + (y - 3)^2$
$CA^2 = x^2 + 8x + 16 + y^2 - 6y + 9$
$CA^2 = x^2 + y^2 + 8x - 6y + 25$
Equate $CA^2$ to $AB^2 = 64$:
$x^2 + y^2 + 8x - 6y + 25 = 64$
... (2)
Subtract equation (1) from equation (2):
$(x^2 + y^2 + 8x - 6y + 25) - (x^2 + y^2 - 8x - 6y + 25) = 64 - 64$
$x^2 - x^2 + y^2 - y^2 + 8x - (-8x) - 6y - (-6y) + 25 - 25 = 0$
$8x + 8x - 6y + 6y + 0 = 0$
$16x = 0$
$x = 0$
Substitute $x = 0$ into equation (1):
$(0)^2 + y^2 - 8(0) - 6y + 25 = 64$
$0 + y^2 - 0 - 6y + 25 = 64$
$y^2 - 6y + 25 = 64$
Rearrange into a quadratic equation in y:
$y^2 - 6y + 25 - 64 = 0$
$y^2 - 6y - 39 = 0$
Use the quadratic formula to solve for y: $y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
Here, $a=1$, $b=-6$, $c=-39$.
$y = \frac{-(-6) \pm \sqrt{(-6)^2 - 4(1)(-39)}}{2(1)}$
$y = \frac{6 \pm \sqrt{36 + 156}}{2}$
$y = \frac{6 \pm \sqrt{192}}{2}$
Simplify $\sqrt{192}$. $192 = 64 \times 3$.
$y = \frac{6 \pm \sqrt{64 \times 3}}{2}$
$y = \frac{6 \pm 8\sqrt{3}}{2}$
Divide both terms in the numerator by 2:
$y = 3 \pm 4\sqrt{3}$
This gives two possible y-coordinates for the third vertex, with $x=0$. The two possible locations for the third vertex are $(0, 3 + 4\sqrt{3})$ and $(0, 3 - 4\sqrt{3})$.
We are given that the origin (0, 0) lies in the interior of the triangle.
The base AB is a horizontal line at $y = 3$. The vertices A and B are at $x = -4$ and $x = 4$.
The origin (0, 0) is below the line $y = 3$. For the origin to be inside the triangle, the third vertex C must be on the opposite side of the line AB from the origin.
Points with y-coordinate less than 3 are on the same side as the origin relative to the line $y=3$. Points with y-coordinate greater than 3 are on the opposite side.
Consider the two possible y-coordinates:
$y_1 = 3 + 4\sqrt{3}$. Since $\sqrt{3} \approx 1.732$, $4\sqrt{3} \approx 6.928$. So $y_1 \approx 3 + 6.928 = 9.928$. This value is greater than 3.
$y_2 = 3 - 4\sqrt{3} \approx 3 - 6.928 = -3.928$. This value is less than 3.
For the origin (0, 0) to be in the interior of the triangle, the third vertex must be on the opposite side of the base AB (the line $y=3$). Since the origin is below $y=3$, the third vertex must be above $y=3$. This means the y-coordinate of the third vertex must be greater than 3.
Therefore, the correct y-coordinate is $y = 3 + 4\sqrt{3}$.
The coordinates of the third vertex are $(0, 3 + 4\sqrt{3})$.
The coordinates of the third vertex are $(0, 3 + 4\sqrt{3})$.
Question 2. A (6, 1), B (8, 2) and C (9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of Δ ADE.
Answer:
Given:
Vertices A (6, 1), B (8, 2), and C (9, 4) of a parallelogram ABCD.
E is the mid-point of side DC.
To Find:
The area of Δ ADE.
Solution:
First, we need to find the coordinates of the fourth vertex D of the parallelogram ABCD.
Let the coordinates of D be $(x_D, y_D)$.
In a parallelogram, the diagonals bisect each other. The midpoint of AC is the same as the midpoint of BD.
Midpoint of AC using A(6, 1) and C(9, 4):
Midpoint x-coordinate $= \frac{6 + 9}{2} = \frac{15}{2}$
Midpoint y-coordinate $= \frac{1 + 4}{2} = \frac{5}{2}$
Midpoint of AC is $\left(\frac{15}{2}, \frac{5}{2}\right)$.
Midpoint of BD using B(8, 2) and D$(x_D, y_D)$:
Midpoint x-coordinate $= \frac{8 + x_D}{2}$
Midpoint y-coordinate $= \frac{2 + y_D}{2}$
Equate the coordinates of the midpoints:
$\frac{8 + x_D}{2} = \frac{15}{2} \implies 8 + x_D = 15 \implies x_D = 15 - 8 = 7$
$\frac{2 + y_D}{2} = \frac{5}{2} \implies 2 + y_D = 5 \implies y_D = 5 - 2 = 3$
The coordinates of vertex D are (7, 3).
Next, we need to find the coordinates of point E, the midpoint of DC.
D (7, 3) and C (9, 4).
Midpoint E x-coordinate $= \frac{7 + 9}{2} = \frac{16}{2} = 8$
Midpoint E y-coordinate $= \frac{3 + 4}{2} = \frac{7}{2}$
The coordinates of point E are $\left(8, \frac{7}{2}\right)$.
Now, we find the area of Δ ADE with vertices A (6, 1), D (7, 3), and E $\left(8, \frac{7}{2}\right)$.
Let the coordinates of the vertices be:
$A(x_1, y_1) = (6, 1)$
$D(x_2, y_2) = (7, 3)$
$E(x_3, y_3) = \left(8, \frac{7}{2}\right)$
The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by the formula:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Substitute the coordinates of A, D, and E into the formula:
Area(ADE) $= \frac{1}{2} \left| 6\left(3 - \frac{7}{2}\right) + 7\left(\frac{7}{2} - 1\right) + 8(1 - 3) \right|$
Calculate the terms inside the absolute value:
$3 - \frac{7}{2} = \frac{6}{2} - \frac{7}{2} = -\frac{1}{2}$
$\frac{7}{2} - 1 = \frac{7}{2} - \frac{2}{2} = \frac{5}{2}$
$1 - 3 = -2$
Substitute these values back into the area formula:
Area(ADE) $= \frac{1}{2} \left| 6\left(-\frac{1}{2}\right) + 7\left(\frac{5}{2}\right) + 8(-2) \right|$
Area(ADE) $= \frac{1}{2} \left| -3 + \frac{35}{2} - 16 \right|$
Area(ADE) $= \frac{1}{2} \left| -19 + \frac{35}{2} \right|$
Area(ADE) $= \frac{1}{2} \left| -\frac{38}{2} + \frac{35}{2} \right|$
Area(ADE) $= \frac{1}{2} \left| \frac{-3}{2} \right|$
Area(ADE) $= \frac{1}{2} \times \frac{3}{2} = \frac{3}{4}$ square units.
Alternate Approach:
In parallelogram ABCD, the diagonal AC divides it into two triangles of equal area, Area(ABC) = Area(ADC).
Area(ABC) using A(6, 1), B(8, 2), C(9, 4):
Area(ABC) $= \frac{1}{2} |6(2 - 4) + 8(4 - 1) + 9(1 - 2)|$
Area(ABC) $= \frac{1}{2} |6(-2) + 8(3) + 9(-1)|$
Area(ABC) $= \frac{1}{2} |-12 + 24 - 9|$
Area(ABC) $= \frac{1}{2} |12 - 9|$
Area(ABC) $= \frac{1}{2} |3| = \frac{3}{2}$ square units.
Area(ADC) = Area(ABC) = $\frac{3}{2}$ square units.
In Δ ADC, E is the midpoint of DC. The line segment AE is a median of Δ ADC.
A median of a triangle divides it into two triangles of equal area.
Area(ADE) $= \frac{1}{2} \times$ Area(ADC)
Area(ADE) $= \frac{1}{2} \times \frac{3}{2} = \frac{3}{4}$ square units.
The area of Δ ADE is $\frac{3}{4}$ square units.
Question 3. The points A (x1, y1), B (x2 , y2) and C (x3 y3) are the vertices of Δ ABC.
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1
(iii) Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
(iv) What are the coordinates of the centroid of the triangle ABC?
Answer:
Given:
Vertices of Δ ABC are A $(x_1, y_1)$, B $(x_2, y_2)$, and C $(x_3, y_3)$.
(i) Find the coordinates of the point D, where the median from A meets BC.
Since AD is the median from A to BC, the point D is the midpoint of the side BC.
Using the midpoint formula, the coordinates of D are:
D $(x_D, y_D) = \left(\frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2}\right)$
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
Point P divides the line segment AD internally in the ratio 2 : 1.
Using the section formula for internal division, the coordinates of P $(x_P, y_P)$ dividing the line segment joining A $(x_1, y_1)$ and D $\left(\frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2}\right)$ in the ratio $m : n = 2 : 1$ are:
$x_P = \frac{m x_D + n x_A}{m + n} = \frac{2 \left(\frac{x_2 + x_3}{2}\right) + 1 (x_1)}{2 + 1}$
$x_P = \frac{x_2 + x_3 + x_1}{3} = \frac{x_1 + x_2 + x_3}{3}$
$y_P = \frac{m y_D + n y_A}{m + n} = \frac{2 \left(\frac{y_2 + y_3}{2}\right) + 1 (y_1)}{2 + 1}$
$y_P = \frac{y_2 + y_3 + y_1}{3} = \frac{y_1 + y_2 + y_3}{3}$
The coordinates of point P are $\left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right)$.
(iii) Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
Let E be the midpoint of AC. Coordinates of E $(x_E, y_E) = \left(\frac{x_1 + x_3}{2}, \frac{y_1 + y_3}{2}\right)$.
Point Q divides the median BE (from B $(x_2, y_2)$ to E $\left(\frac{x_1 + x_3}{2}, \frac{y_1 + y_3}{2}\right)$) in the ratio 2 : 1.
Using the section formula for internal division, the coordinates of Q $(x_Q, y_Q)$ are:
$x_Q = \frac{m x_E + n x_B}{m + n} = \frac{2 \left(\frac{x_1 + x_3}{2}\right) + 1 (x_2)}{2 + 1}$
$x_Q = \frac{x_1 + x_3 + x_2}{3} = \frac{x_1 + x_2 + x_3}{3}$
$y_Q = \frac{m y_E + n y_B}{m + n} = \frac{2 \left(\frac{y_1 + y_3}{2}\right) + 1 (y_2)}{2 + 1}$
$y_Q = \frac{y_1 + y_3 + y_2}{3} = \frac{y_1 + y_2 + y_3}{3}$
The coordinates of point Q are $\left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right)$.
Let F be the midpoint of AB. Coordinates of F $(x_F, y_F) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Point R divides the median CF (from C $(x_3, y_3)$ to F $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$) in the ratio 2 : 1.
Using the section formula for internal division, the coordinates of R $(x_R, y_R)$ are:
$x_R = \frac{m x_F + n x_C}{m + n} = \frac{2 \left(\frac{x_1 + x_2}{2}\right) + 1 (x_3)}{2 + 1}$
$x_R = \frac{x_1 + x_2 + x_3}{3} = \frac{x_1 + x_2 + x_3}{3}$
$y_R = \frac{m y_F + n y_C}{m + n} = \frac{2 \left(\frac{y_1 + y_2}{2}\right) + 1 (y_3)}{2 + 1}$
$y_R = \frac{y_1 + y_2 + y_3}{3} = \frac{y_1 + y_2 + y_3}{3}$
The coordinates of point R are $\left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right)$.
(iv) What are the coordinates of the centroid of the triangle ABC?
From parts (ii) and (iii), we found that points P, Q, and R all have the same coordinates: $\left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right)$.
These points lie on the medians AD, BE, and CF respectively, and divide each median in the ratio 2:1 from the vertex.
The point of intersection of the medians of a triangle is called the centroid. The centroid divides each median in the ratio 2:1.
Therefore, the points P, Q, and R are the same point, which is the centroid of Δ ABC.
The coordinates of the centroid of the triangle ABC are given by the formula:
Centroid $= \left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right)$
The coordinates of the centroid of the triangle ABC are $\left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right)$.
Question 4. If the points A (1, –2), B (2, 3) C (a, 2) and D (– 4, –3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base.
Answer:
Given:
The points A (1, –2), B (2, 3), C (a, 2), and D (– 4, –3) form a parallelogram ABCD.
AB is taken as the base of the parallelogram.
To Find:
The value of a.
The height of the parallelogram taking AB as base.
Solution:
In a parallelogram, the diagonals bisect each other. The midpoint of AC is the same as the midpoint of BD.
Midpoint of AC using A(1, –2) and C(a, 2):
Midpoint x-coordinate $= \frac{1 + a}{2}$
Midpoint y-coordinate $= \frac{-2 + 2}{2} = \frac{0}{2} = 0$
Midpoint of AC is $\left(\frac{1 + a}{2}, 0\right)$.
Midpoint of BD using B(2, 3) and D(– 4, –3):
Midpoint x-coordinate $= \frac{2 + (-4)}{2} = \frac{2 - 4}{2} = \frac{-2}{2} = -1$
Midpoint y-coordinate $= \frac{3 + (-3)}{2} = \frac{3 - 3}{2} = \frac{0}{2} = 0$
Midpoint of BD is $(-1, 0)$.
Equate the coordinates of the midpoints:
$\frac{1 + a}{2} = -1$
$1 + a = -1 \times 2$
$1 + a = -2$
$a = -2 - 1 = -3$
The value of a is -3.
The coordinates of vertex C are (–3, 2).
Now, we need to find the height of the parallelogram taking AB as the base. The height is the perpendicular distance from either C or D to the line containing the segment AB.
First, find the equation of the line AB.
Points A (1, –2) and B (2, 3).
Slope of AB $(m) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{3 - (-2)}{2 - 1} = \frac{3 + 2}{1} = 5$
Using the point-slope form of the equation of a line $y - y_1 = m(x - x_1)$ with point A(1, -2) and slope m=5:
$y - (-2) = 5(x - 1)$
$y + 2 = 5x - 5$
$5x - y - 5 - 2 = 0$
$5x - y - 7 = 0$
... (Equation of line AB)
The height of the parallelogram is the perpendicular distance from point D (–4, –3) to the line $5x - y - 7 = 0$.
The formula for the perpendicular distance from a point $(x_0, y_0)$ to a line $Ax + By + C = 0$ is $\frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$.
Here, $(x_0, y_0) = (-4, -3)$, and the line is $5x - y - 7 = 0$, so $A=5$, $B=-1$, $C=-7$.
Height $= \frac{|5(-4) + (-1)(-3) - 7|}{\sqrt{5^2 + (-1)^2}}$
Height $= \frac{|-20 + 3 - 7|}{\sqrt{25 + 1}}$
Height $= \frac{|-17 - 7|}{\sqrt{26}}$
Height $= \frac{|-24|}{\sqrt{26}}$
Height $= \frac{24}{\sqrt{26}}$
We can rationalize the denominator:
Height $= \frac{24}{\sqrt{26}} \times \frac{\sqrt{26}}{\sqrt{26}} = \frac{24\sqrt{26}}{26} = \frac{12\sqrt{26}}{13}$ units.
We can also calculate the length of the base AB.
$A = (1, -2)$, $B = (2, 3)$
$AB = \sqrt{(2 - 1)^2 + (3 - (-2))^2} = \sqrt{1^2 + 5^2} = \sqrt{1 + 25} = \sqrt{26}$ units.
Area of parallelogram = base $\times$ height.
Area of parallelogram ABCD is also $2 \times$ Area(ABD).
Vertices A(1, -2), B(2, 3), D(-4, -3).
Area(ABD) $= \frac{1}{2} |1(3 - (-3)) + 2(-3 - (-2)) + (-4)(-2 - 3)|$
Area(ABD) $= \frac{1}{2} |1(6) + 2(-1) + (-4)(-5)|$
Area(ABD) $= \frac{1}{2} |6 - 2 + 20|$
Area(ABD) $= \frac{1}{2} |4 + 20|$
Area(ABD) $= \frac{1}{2} |24| = 12$ square units.
Area of parallelogram ABCD $= 2 \times 12 = 24$ square units.
Area = base $\times$ height
$24 = \sqrt{26} \times \text{height}$
Height $= \frac{24}{\sqrt{26}}$, which matches the distance calculation.
The value of a is -3.
The height of the parallelogram taking AB as base is $\frac{24}{\sqrt{26}}$ or $\frac{12\sqrt{26}}{13}$ units.
Question 5. Students of a school are standing in rows and columns in their playground for a drill practice. A, B, C and D are the positions of four students as shown in figure 7.4. Is it possible to place Jaspal in the drill in such a way that he is equidistant from each of the four students A, B, C and D? If so, what should be his position?
Answer:
Given:
The positions of four students are given by the points A, B, C, and D in the figure.
To Find:
Whether it is possible to place a point Jaspal equidistant from A, B, C, and D.
If possible, the coordinates of Jaspal's position.
Solution:
From the given figure, the coordinates of the four students are:
A $(3, 2)$
B $(6, 5)$
C $(9, 2)$
D $(6, -1)$
A point equidistant from four points A, B, C, and D is the center of the circle that passes through all four points (the circumcenter). Such a point exists if and only if the four points are concyclic (lie on the same circle), forming a cyclic quadrilateral.
Let's examine the type of quadrilateral formed by these points by calculating the lengths of the sides using the distance formula $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Length of AB:
$AB = \sqrt{(6 - 3)^2 + (5 - 2)^2} = \sqrt{3^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}$
Length of BC:
$BC = \sqrt{(9 - 6)^2 + (2 - 5)^2} = \sqrt{3^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}$
Length of CD:
$CD = \sqrt{(6 - 9)^2 + (-1 - 2)^2} = \sqrt{(-3)^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}$
Length of DA:
$DA = \sqrt{(3 - 6)^2 + (2 - (-1))^2} = \sqrt{(-3)^2 + (2 + 1)^2} = \sqrt{(-3)^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}$
Since $AB = BC = CD = DA$, all four sides are equal in length. This indicates the quadrilateral is either a rhombus or a square.
Now, let's calculate the lengths of the diagonals AC and BD.
Length of AC:
$AC = \sqrt{(9 - 3)^2 + (2 - 2)^2} = \sqrt{6^2 + 0^2} = \sqrt{36} = 6$
Length of BD:
$BD = \sqrt{(6 - 6)^2 + (-1 - 5)^2} = \sqrt{0^2 + (-6)^2} = \sqrt{36} = 6$
Since $AC = BD$, the diagonals are equal in length.
A quadrilateral with all four sides equal and equal diagonals is a square.
A square is a cyclic quadrilateral, meaning its vertices lie on a circle. The center of this circle (the circumcenter) is equidistant from all four vertices.
The circumcenter of a square is the midpoint of its diagonals.
Let's find the midpoint of the diagonal AC using the midpoint formula $\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)$.
Midpoint of AC $= \left(\frac{3 + 9}{2}, \frac{2 + 2}{2}\right) = \left(\frac{12}{2}, \frac{4}{2}\right) = (6, 2)$
We can verify by finding the midpoint of the other diagonal BD.
Midpoint of BD $= \left(\frac{6 + 6}{2}, \frac{5 + (-1)}{2}\right) = \left(\frac{12}{2}, \frac{4}{2}\right) = (6, 2)$
Both diagonals have the same midpoint, which is $(6, 2)$.
This point $(6, 2)$ is the circumcenter of the square ABCD and is therefore equidistant from all four vertices A, B, C, and D.
Thus, it is possible to place Jaspal such that he is equidistant from each of the four students.
Jaspal's position should be at the coordinates of the circumcenter, which is $(6, 2)$.
Yes, it is possible to place Jaspal such that he is equidistant from each of the four students A, B, C, and D.
His position should be at (6, 2).
Question 6. Ayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughter’s school and then reaches the office. What is the extra distance travelled by Ayush in reaching his office? (Assume that all distances covered are in straight lines).
If the house is situated at (2, 4), bank at (5, 8), school at (13, 14) and office at (13, 26) and coordinates are in km.
Answer:
Given:
House (H) is at (2, 4).
Bank (B) is at (5, 8).
School (S) is at (13, 14).
Office (O) is at (13, 26).
Ayush's path is H $\to$ B $\to$ S $\to$ O.
The direct path is H $\to$ O.
Coordinates are in km.
To Find:
The extra distance travelled by Ayush.
Solution:
We need to calculate the total distance travelled by Ayush on his indirect path (HB + BS + SO) and the distance of the direct path (HO).
The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the distance formula $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Calculate the distance from House (2, 4) to Bank (5, 8) - HB:
$HB = \sqrt{(5 - 2)^2 + (8 - 4)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$ km.
Calculate the distance from Bank (5, 8) to School (13, 14) - BS:
$BS = \sqrt{(13 - 5)^2 + (14 - 8)^2} = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10$ km.
Calculate the distance from School (13, 14) to Office (13, 26) - SO:
Note that the x-coordinates of S and O are the same (13). This means the path SO is a vertical line. The distance is the absolute difference in y-coordinates.
$SO = \sqrt{(13 - 13)^2 + (26 - 14)^2} = \sqrt{0^2 + 12^2} = \sqrt{144} = 12$ km.
Total distance travelled on the indirect path = $HB + BS + SO = 5 + 10 + 12 = 27$ km.
Calculate the distance of the direct path from House (2, 4) to Office (13, 26) - HO:
$HO = \sqrt{(13 - 2)^2 + (26 - 4)^2} = \sqrt{11^2 + 22^2} = \sqrt{121 + 484} = \sqrt{605}$
To simplify $\sqrt{605}$, find its prime factorization. $605 = 5 \times 121 = 5 \times 11^2$.
$HO = \sqrt{11^2 \times 5} = 11\sqrt{5}$ km.
Using $\sqrt{5} \approx 2.236$, the direct distance is approximately $11 \times 2.236 = 24.596$ km.
The extra distance travelled by Ayush is the difference between the indirect distance and the direct distance.
Extra distance = (HB + BS + SO) - HO
Extra distance = $27 - 11\sqrt{5}$ km.
If we need a numerical approximation for the extra distance:
Extra distance $\approx 27 - 24.596 = 2.404$ km.
The extra distance travelled by Ayush is $(27 - 11\sqrt{5})$ km. (Approximately 2.404 km).

